Today's Progress 14. Jan. 2008

Generalized acceptance of &Lambda d spectra (1)

As has been discussed here, acceptance as the single variable function of mass must be process-dependent even for 3-body final states, and more general expression is absolutely needed to perform correction for arbitrary process in an unified scheme. Here, we try to perform generalized acceptance correction for &Lambda d spectra, to demonstrate the easiest case, firstly. The numerical factor for the normalization is discussed in the folowing document.
  • ld_acc_corr.pdf - Acceptance correction scheme of Lambda d spectra

    • Evaluation of the acceptance matrix (1)

    Here, we try to evaluate the acceptance function for &Lambda d measurement as the first example of the acceptance correction of YN/Yd spectra.

    Conditions of the Monte-Carlo(1).
    software GEANT3.21
    generated K-+4He at rest
    generated final state &Lambda d n/&Sigma0 d n = 50%:50%
    dynamics(matrix evaluation) uniform on 3-body phase space with 2.0*109 events
    dynamics(dummy data) (K-+4He)->3S++n ,3S+->Y0+d / (K-+4He)->2S0+d ,2S0->Y0+n :: &Lambda : &Sigma0=50:50
    generated event number 2.5*108(phase space)/2.0*107/10 MeV/c2(multibaryons)
    target center (-0.3,0.,1.3):E549
    x/y generation point distribution 4.0 cm sigma Gaussian centered at (x,y)=(-0.3,0.)
    z generation point distribution uniform
    multiple scattering on(Moliere)
    energy loss straggling on(Gauss/Landau/Vavilov are internally selected adequately)
    nuclear reaction of d/p/&pi on(GHEISHA)
    coincidense time gate for PA-PB 45 nsec
    Birk's coefficient for plastic scintillator0.013/(MeV/cm)
    Time resolution of PA/PB for p/d/&pi 60/80 psec
    Convoluted time resolution of TC_B+PA for p/&pi 250 psec
    Analysis inefficiency for p/d/&pi selectionp:properly simulated / d:properly simulated / &pi:neglected
    Analysis inefficiency for p/d/&pi energy-loss correctionNot simulated
    Analysis inefficiency for &Lambda reconstruction by p&pi invariant-mass gateNot simulated
    bin widths 10 MeV/c for p&Lambda and pd, 0.05 for cos&theta&Lambda d,10 MeV/c2 for M&Lambda d and M2S0

    In order to evaluate the function practically, we divide p&Lambda, pd, cos&theta&Lambda d into finite number of bins. Then, the acceptance matrix, &epsilon(p&Lambda , pd , cos&theta&Lambda d) is defined as

    &epsilon(p&Lambda , pd , cos&theta&Lambda d)=D(p&Lambda , pd , cos&theta&Lambda d)/G(p&Lambda , pd , cos&theta&Lambda d),

    where D(p&Lambda , pd , cos&theta&Lambda d),G(p&Lambda , pd , cos&theta&Lambda d) are detected and generated event numbers in each 3-dimensional bin. In a similar way, the acceptance matrix, &epsilon(M&Lambda d , M2S0 , cos&theta&Lambda d) is defined as

    &epsilon(M&Lambda d , M2S0 , cos&theta&Lambda d)=D(M&Lambda d , M2S0 , cos&theta&Lambda d)/G(M&Lambda d , M2S0 , cos&theta&Lambda d),

    which is verified by 1-to-1 correspondance between (p&Lambda,pd,cos&theta&Lambda d) and (M&Lambda d , M2S0 , cos&theta&Lambda d). As a test in the first stage, let we adopt exact values of variables (For the event selection, we use 1/&beta simulated with finite resolutions of PA-PB as in the table). As cos&theta&Lambda d is uniquely determined in &Lambda d n final state if p&Lambda and pd are given, it is impossible to cover whole 3D region where finite event input is expected - hence, we do need &Sigma0 d n final state as well.

    Test with Monte-Carlo data (1)

    Here, we examine three different physics processes for &Lambda/&Sigma0, as

    K- + 4He -> &Lambda + d + n/&Lambda&gamma + d + n (3-body phase space)

    K- + 4He -> 3S+ + n(3S+ production by 2-body phase space) ->&Lambda + d/&Lambda&gamma + d(2-body phase space)

    K- + 4He -> 2S0 + d(2S0 production by 2-body phase space) ->&Lambda + n/&Lambda&gamma + n(2-body phase space)

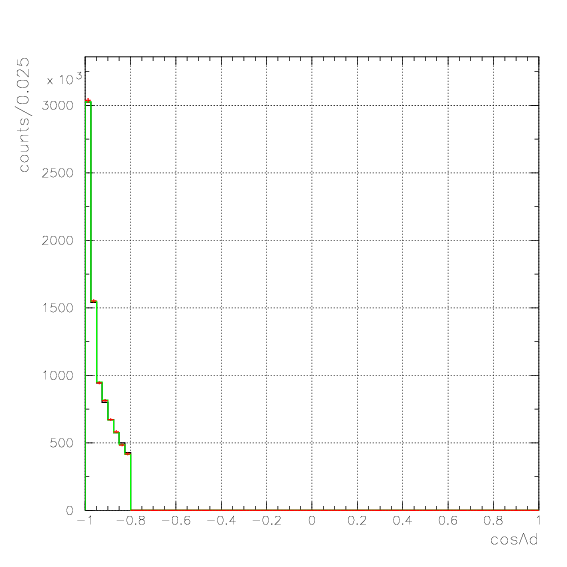
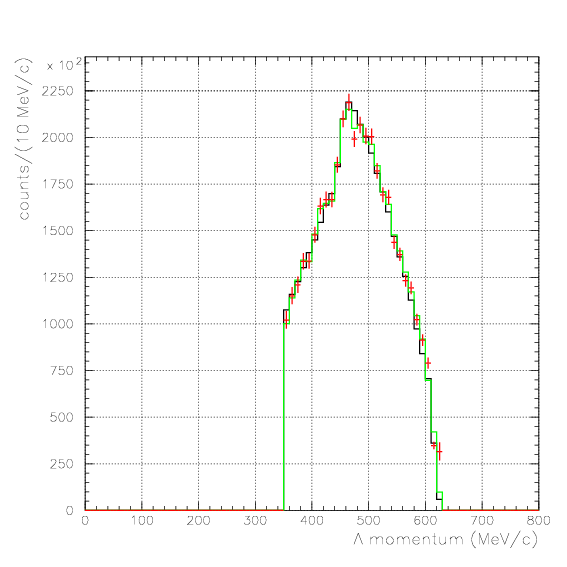
    , and examine the validity of the evaluated acceptance matrix. If we succeed to reconstruct the emitted number spectra from detected ones for all data sets, then the matrix is considered to be appricable to the data. Here, we examine the reproduction of the following five quantities,
  • &Lambda momentum
  • deuteron momentum
  • cos&theta&Lambda d
  • &Lambda d invariant mass
  • 4He(stopped K-,d) 2S0 missing mass
    • for the two different branches of the three simulated prosesses.

    Reproduction and limits of variables

    First of all, we examine the reproduction of the spectra for the condition,

    Pd>470 MeV/c, P&Lambda>280 MeV/c, cos&theta&Lambda d<-0.60

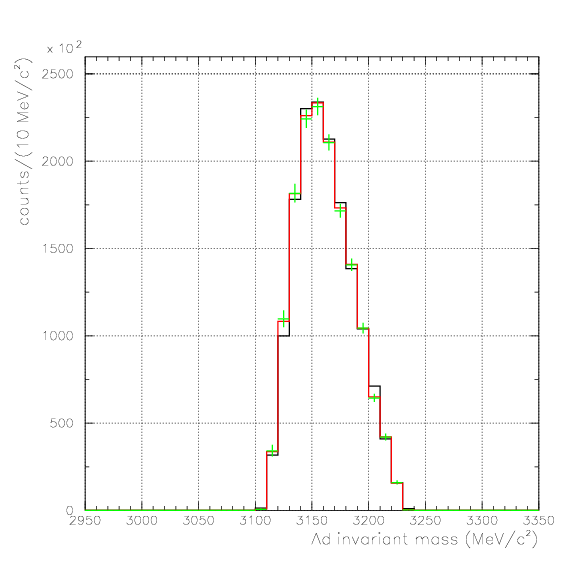
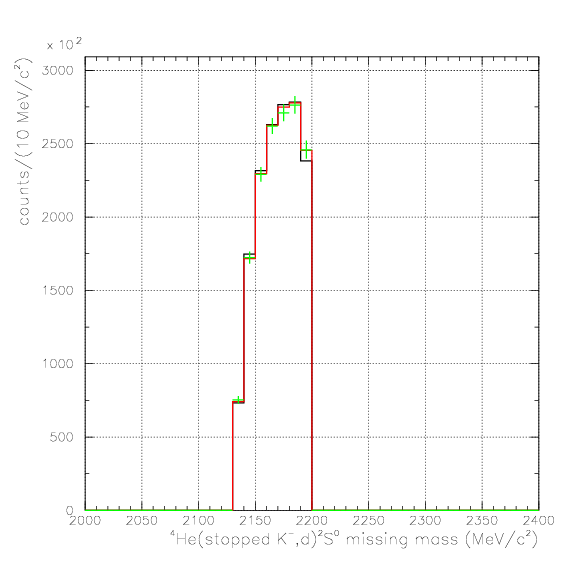
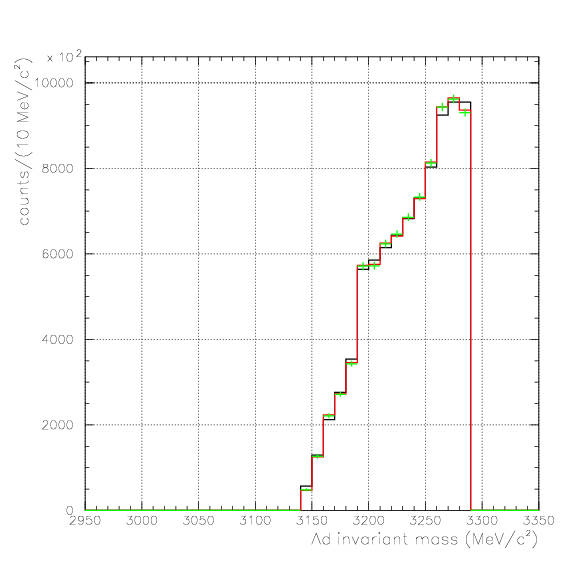
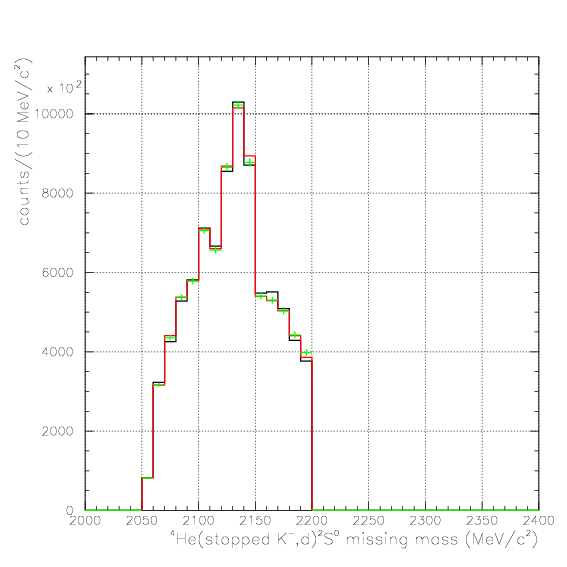
    . Hereafter, the generated and corrected spectra are presented by black and red/green, respectively. The red is used for the acceptance correction with (Pd,P&Lambda, cos&theta&Lambda d), while the green is used for that with (M&Lambda d, M2S,cos&theta&Lambda d), although, the condition is commonly adopted. If the error, which is described just after the section, is well-defined, then they are presented as error bars. As exhibitted below, the strength of the corrected spectra is substantialy lower than the produced ones especially at lower momenta/larger angle - which originates from the contribution from the bins with no detected event.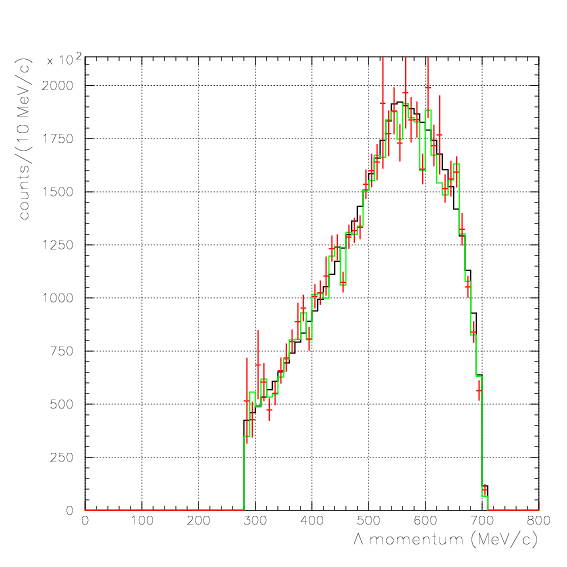
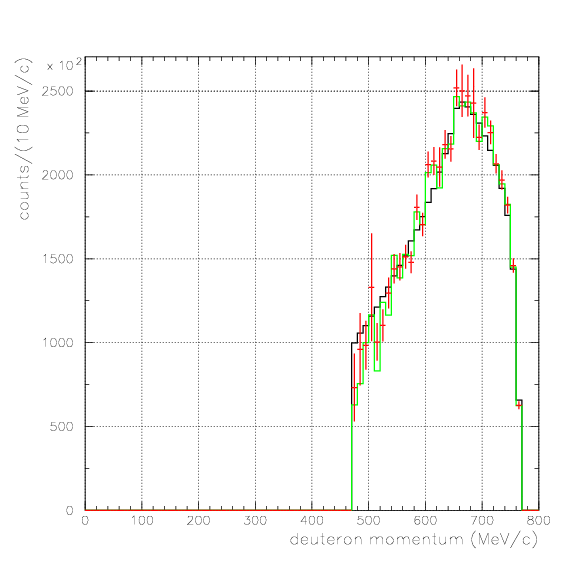
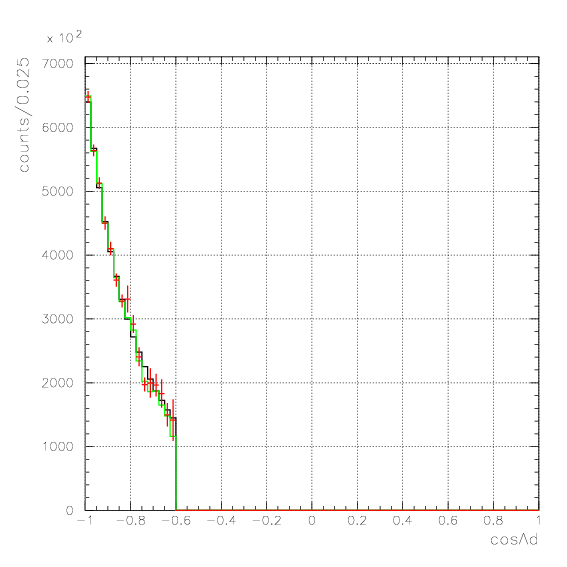
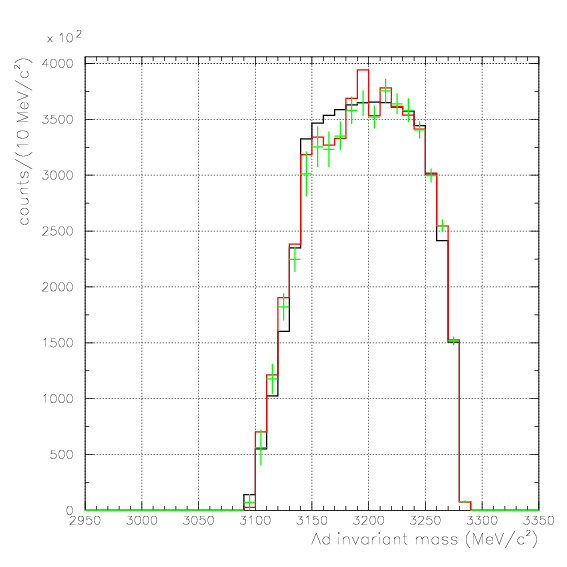
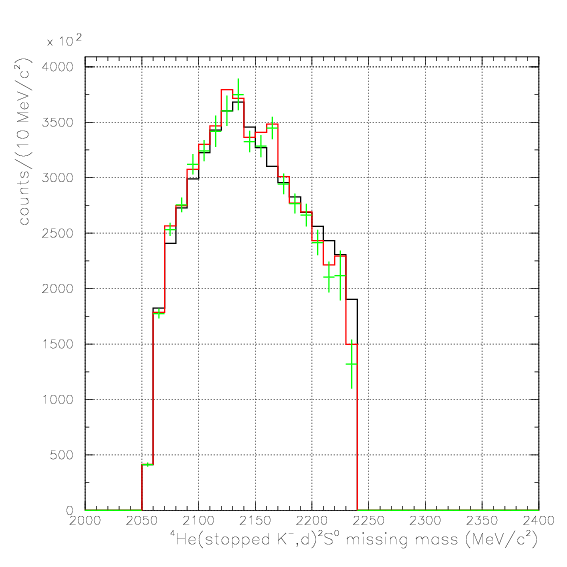
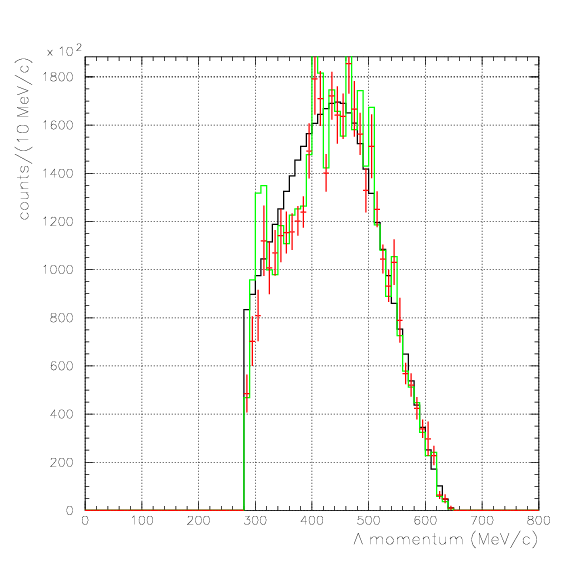
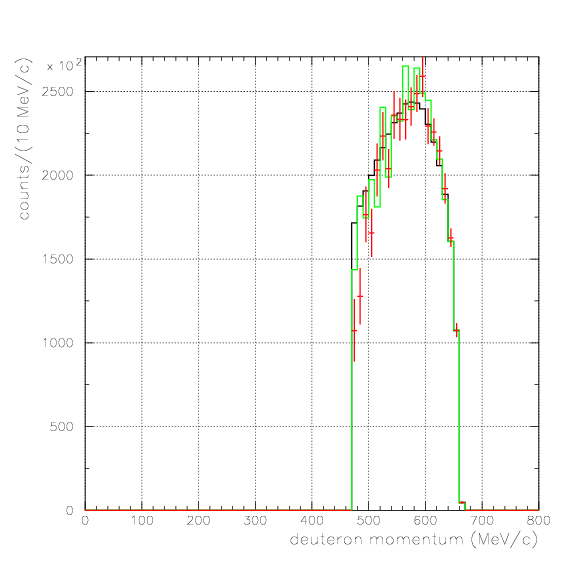
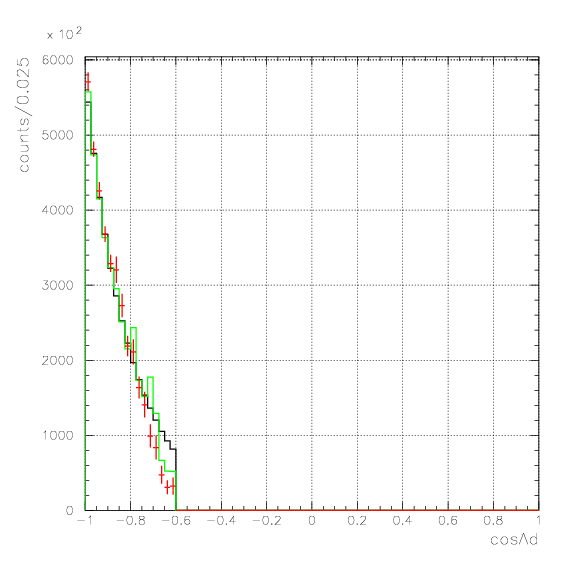
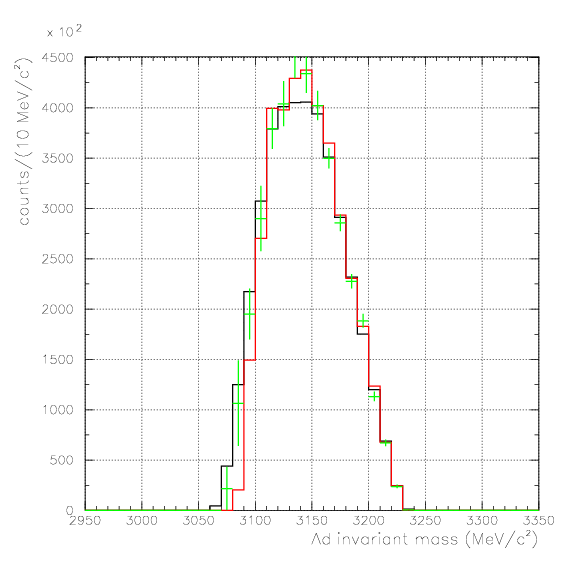
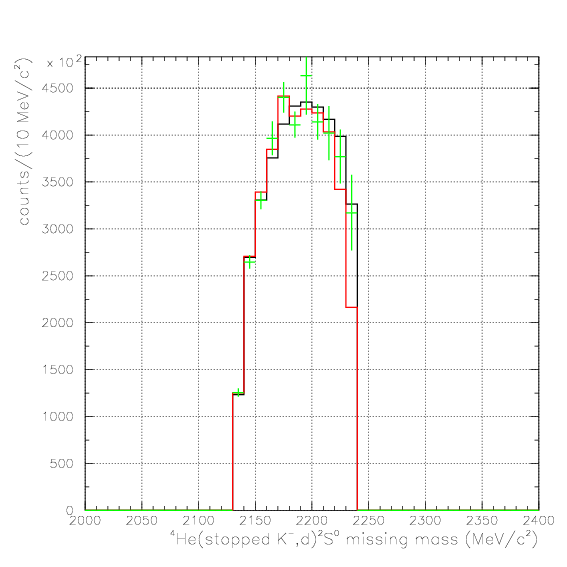
    &Lambda d from &Lambda d n events (phase space)
    &Lambda d from &Sigma0 d n events (phase space)

    Therefore, we must reduce the (Pd, P&Lambda, cos&theta&Lambda d) region to ensure finite number of event contents in all of bins. Hereafter, we reduce the 3D region of the correction to be

    Pd>550 MeV/c, P&Lambda>350 MeV/c, cos&theta&Lambda d<-0.80

    , and examine the acceptance correction for different processes.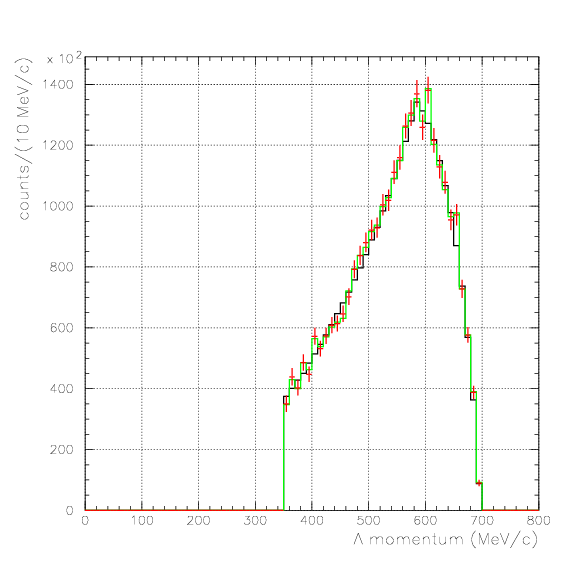

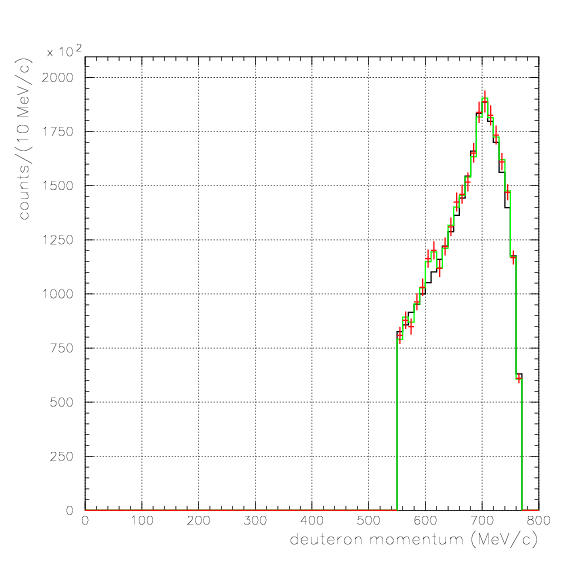
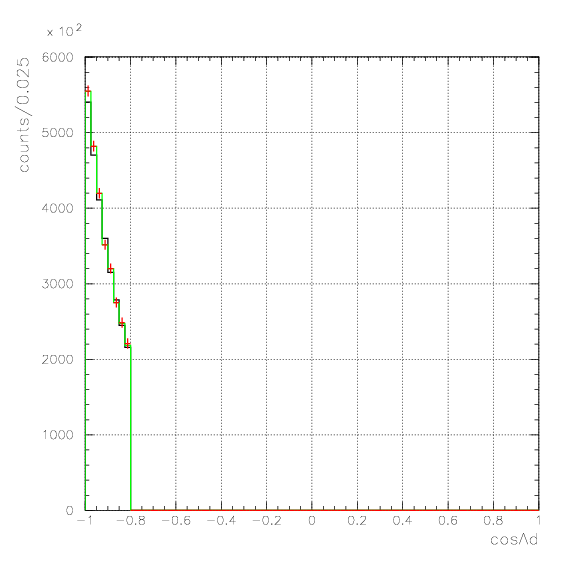
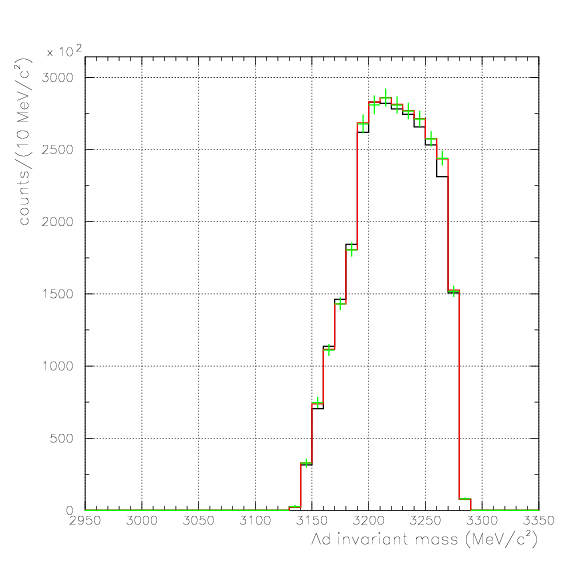
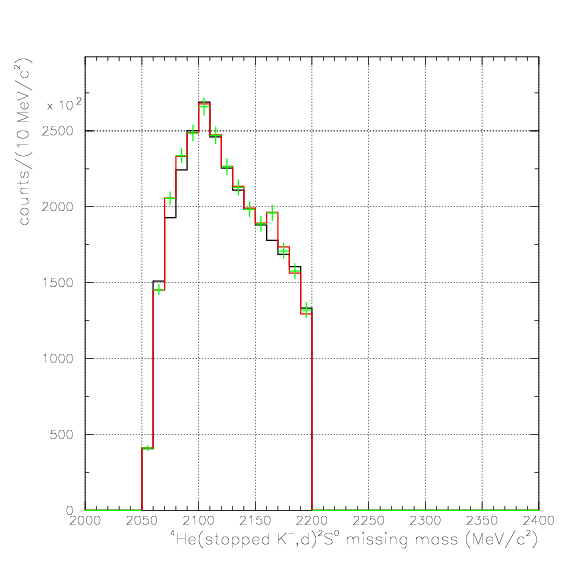
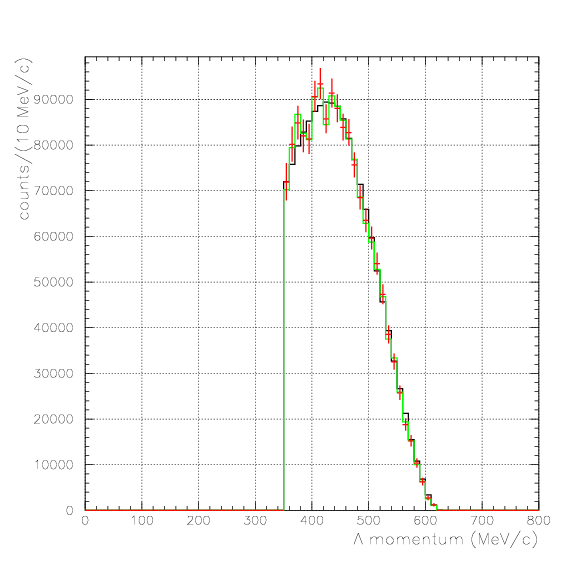
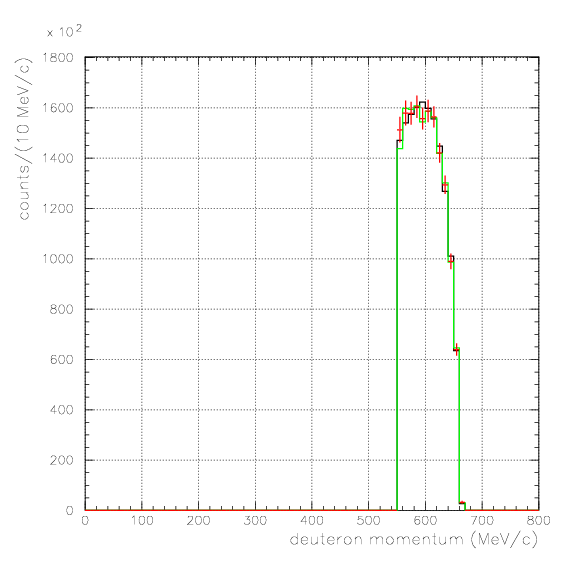
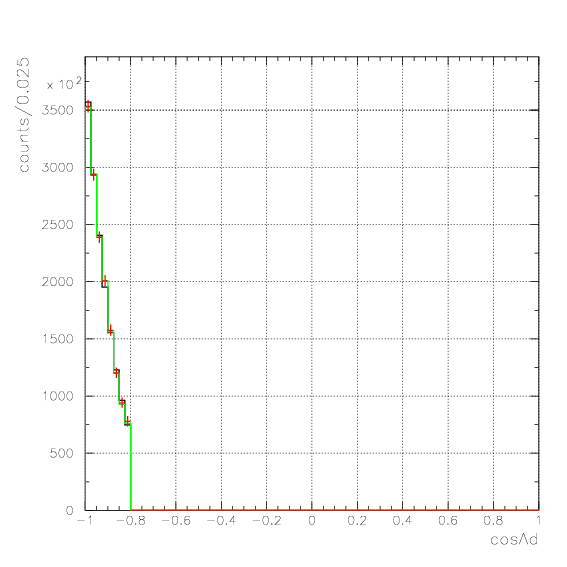
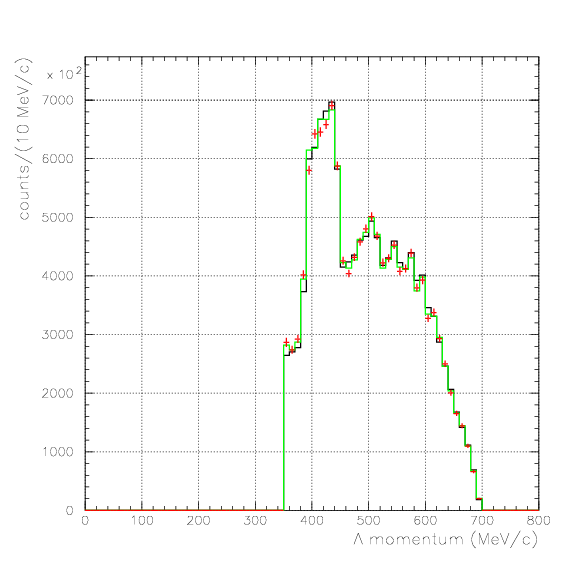
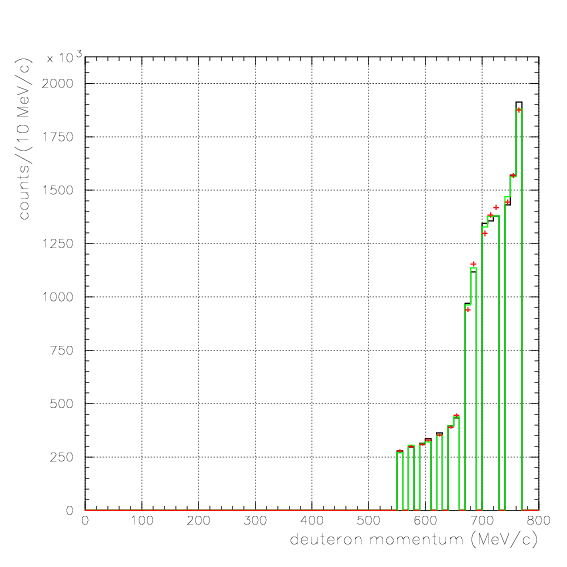
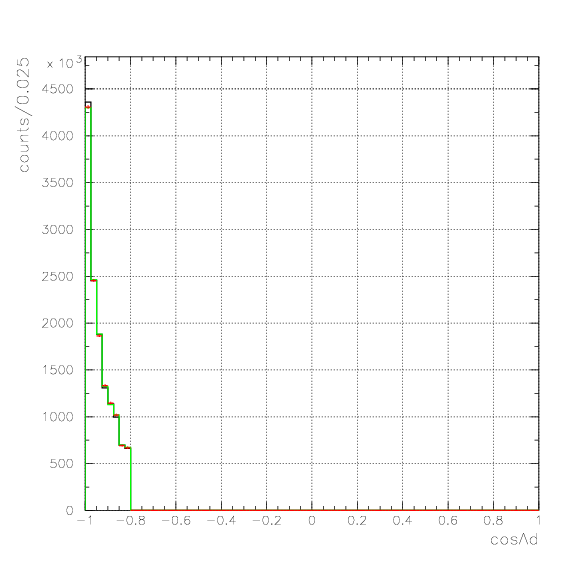
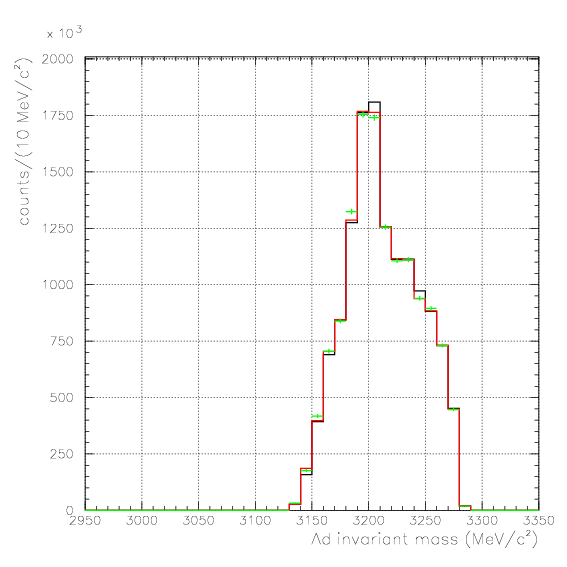
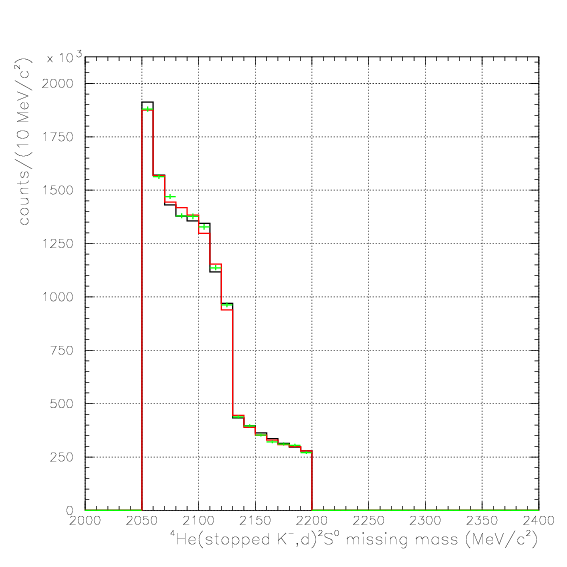
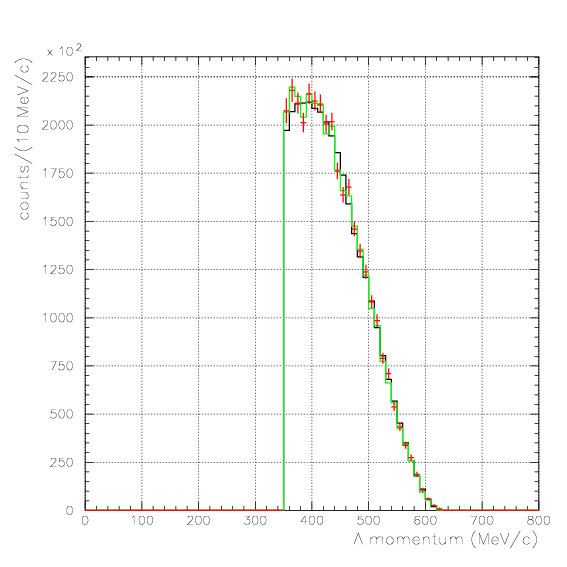
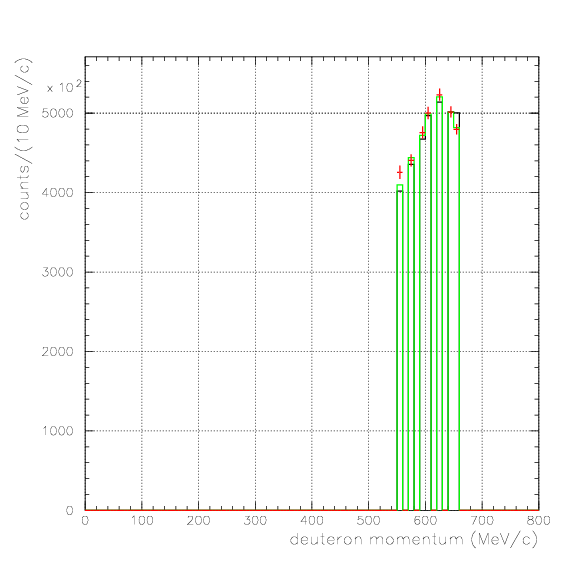
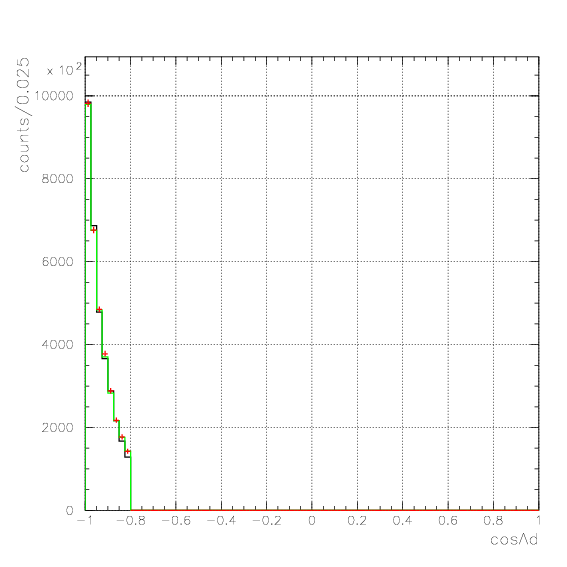
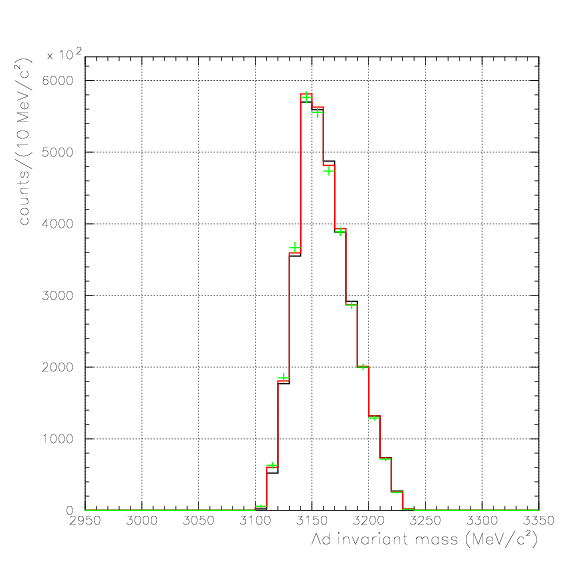
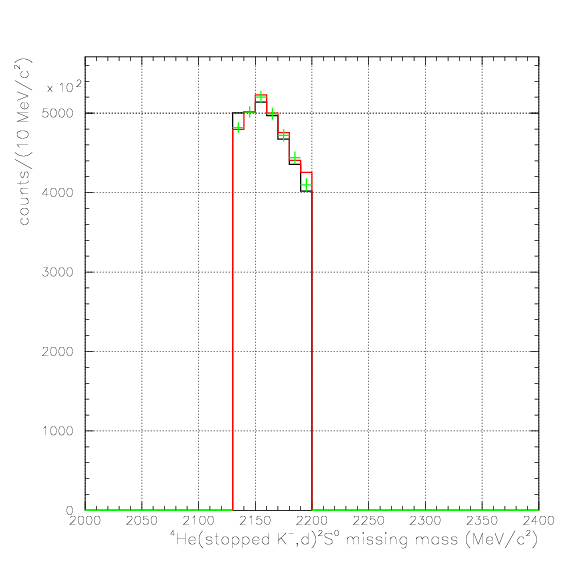
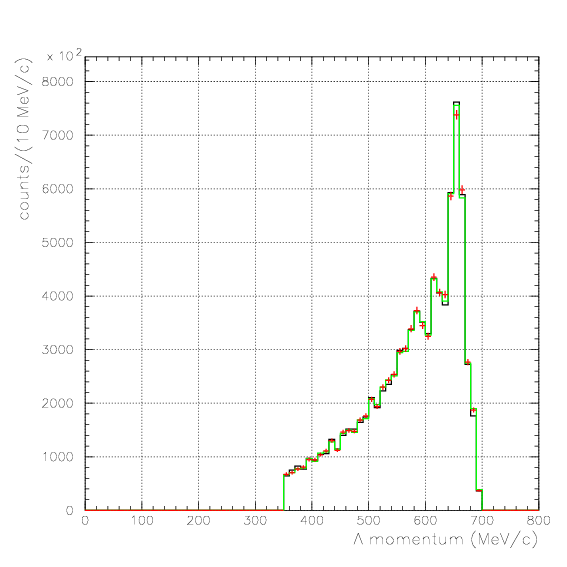
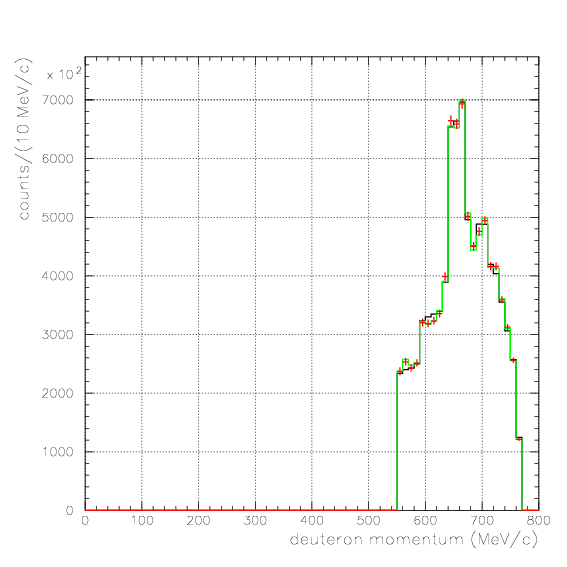
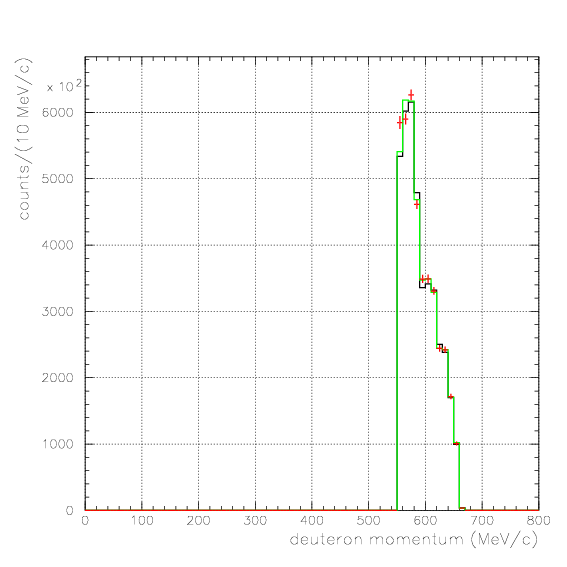
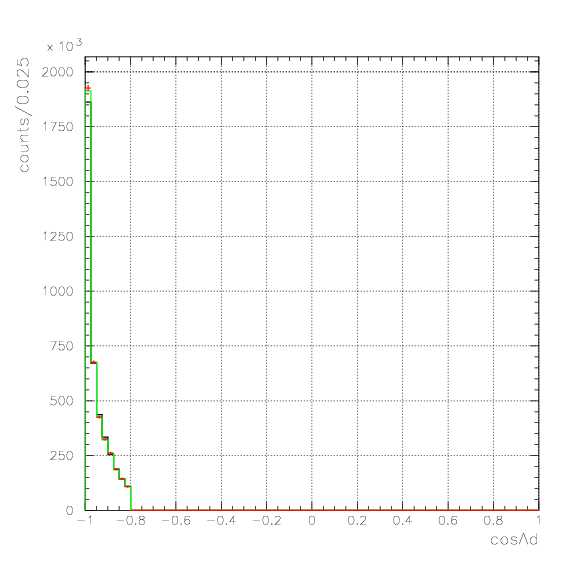
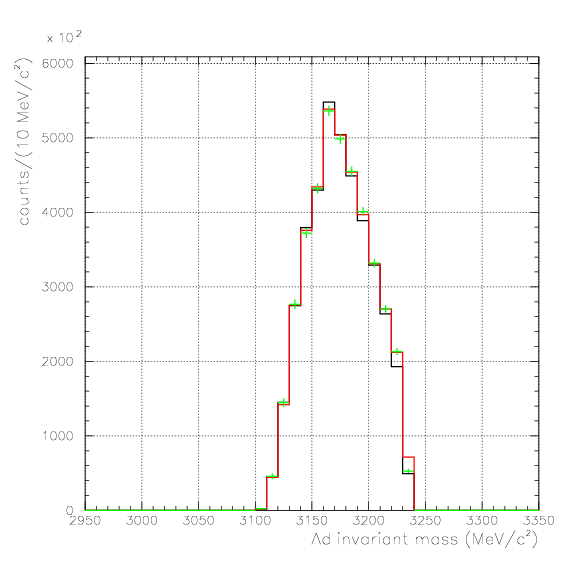
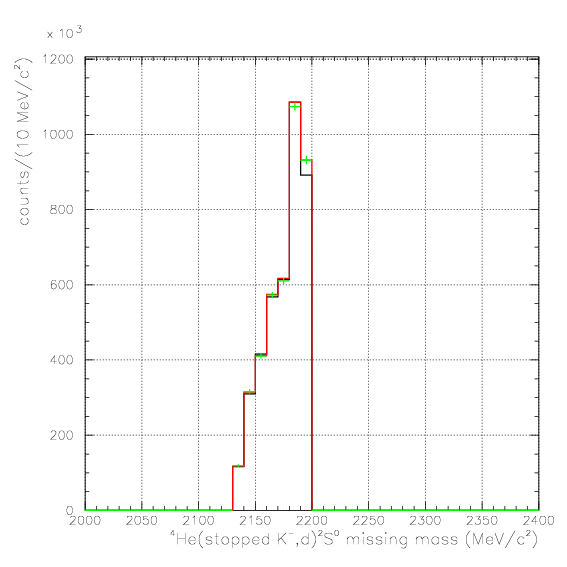
    Three-body phase space (&Lambda d n)

    &Lambda d from &Lambda d n events (phase space)

    Three-body phase space (&Sigma0 d n)

    &Lambda d from &Sigma0 d n events (phase space)

    2S0->&Lambda n

    &Lambda d from X0 d ->(&Lambda n) d events

    2S0->&Sigma0 n

    &Lambda d from X0 d->(&Sigma0 n) d ->(&Lambda &gamma n) d events

    3S+->&Lambda d

    &Lambda d from S+ ->&Lambda d events

    3S+->&Sigma0 d

    &Lambda d from S+ ->&Sigma0 d ->(&Lambda &gamma) d events

    Preliminal conclusion and definition of "error"

    Here, we recognized that the acceptance correction scheme works in principle. However, the reconstruction depends strongly on the total statistics used for the evaluation of the acceptance, and some other method would be required, as will be discussed in the next report. Furthermore, in the real case, definition of the variable region must be considered well taking the very limitted statistics into account. In order to discuss the "error" of each bin in practice, we need some considerations. As the "statistical error" is only defined bin-by-bin of the 3D histgram, we need two acceptance matrixes adopting the variable sets of

    1. Pd, P&Lambda, cos&theta&Lambda d,

    2. M2S0(=4He(stopped K-,d)2S0 missing mass), M&Lambda d, cos&theta&Lambda d,

    which is connected by 1-to-1 corespondance, to allow the error evaluation of projected histgrams. Set 1 is used for the normalization of Pd, P&Lambda, cos&theta&Lambda d, and set 2 is used for M2S0, M&Lambda d, cos&theta&Lambda d, and the bin-by-bin error of variable k, Ek, is evaluated as

    Ek=sqrt(&Sigmai &Sigmaj Cijk/&epsilonijk2),

    which is attributed to the bin contents,

    Ck=&Sigmai &Sigmaj Cijk/&epsilonijk.

    The comparison between original spectra and corrected ones with attributed error was already shown. Hereafter, the definition is always adopted regardless the method of the evaluation of the acceptance matrix and/or the kind of data (i. e. real or simulated data).