Today's Progress 23. Dec. 2007

Yd correlation analysis (2)

By using the clean deuteron events, Yd correlation analysis are exmained here again. Furthermore, direct(i.e. .NOT.compiled from missing hyperon) &Sigma-d correlations are tested, aiming at an unified treatment of Yd spectra.

&Lambda d/&Sigma- d correlation - principle

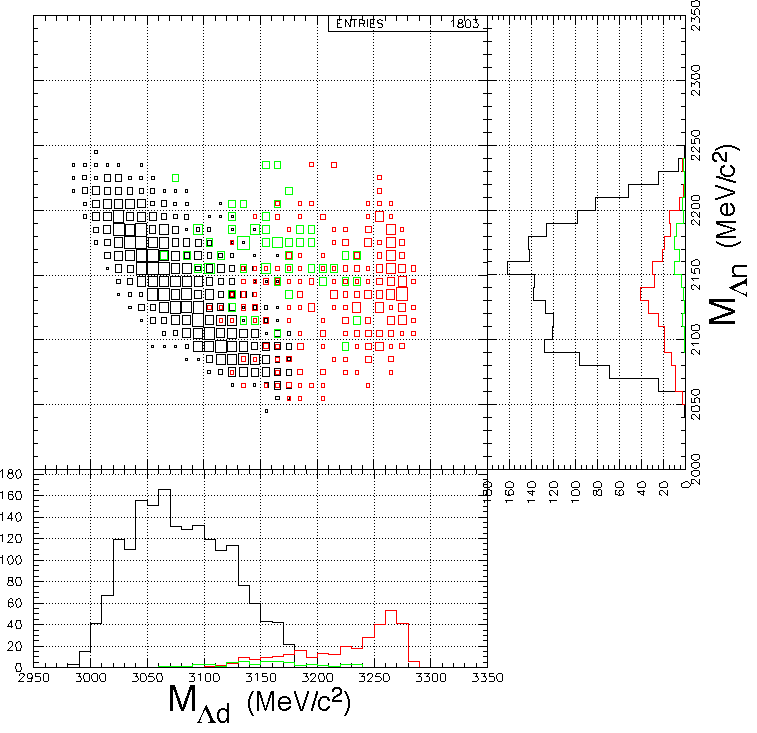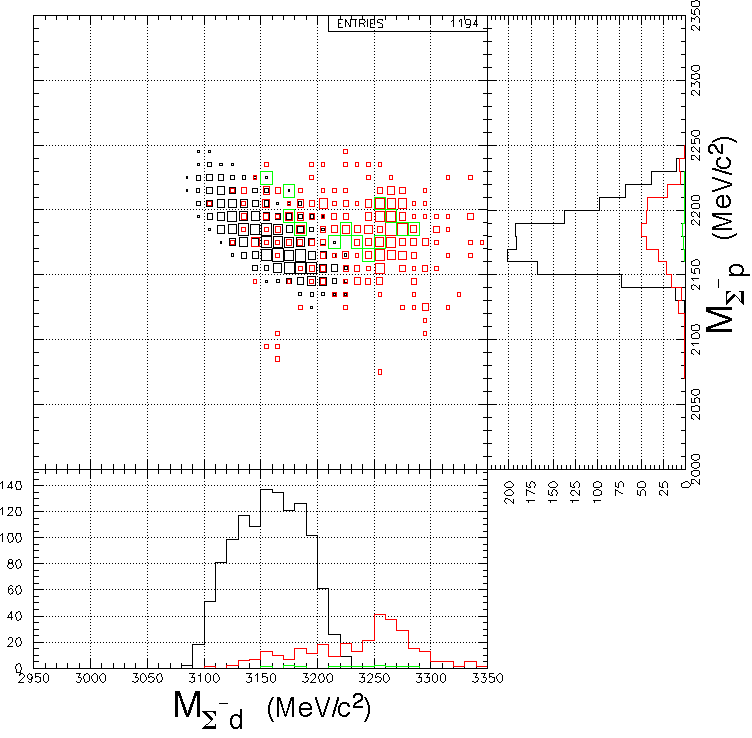
By using &Lambda d/&Sigma- d pairs detected simultaneously, we can study the final state

K- + 4He -> &Lambda + n + d/&Sigma- + p + d.

Even if we detect &Lambda/&Sigma- and d simultaneously, the final state can be contaminated by

K- + 4He -> &Lambda + p + &pi- + d/&Sigma- + p + &pi0 + d,

K- + 4He -> &Lambda + n + &pi0 + d/&Sigma- + n + &pi+ + d,

or

K- + 4He -> &Sigma0(&Lambda&gamma) + n + d,

K- + 4He -> &Sigma0(&Lambda&gamma) + p + &pi- + d,

K- + 4He -> &Sigma0(&Lambda&gamma) + n + &pi0 + d.

The pionic final states are very difficult to be detected due to the small reaction Q-values. All of the contaminants can be eliminated by imposing 4He(stopped K-, d&Lambda)X0/4He(stopped K-, d&Sigma-)X+ missing mass being neutron/proton mass, in principle.

This final state is considered to include known 2 subcomponents, as

K- + "pn" -> &Lambda + n + (d)/&Sigma- + p + (d)----(I):two-nucleon absorption &Lambda n (d)/&Sigma- p (d) branch,

K- + "pn" -> &Lambda + (n) + d/&Sigma- + (p) + d----(II):three-nucleon absorption &Lambda (n) d/&Sigma- (p) d branch,

where spectators in the reactions are in round-brackets, and possible two-more subcomponents,

K- + 4He -> S+(T=0) + n/S0(T=1) + p, S+(T=0)->&Lambda + d/S0(T=1)->&Sigma- + d----(III):S+(T=0)/S0(T=1) tribaryon production and its &Lambda d/&Sigma- d decay,

K- + 4He -> X0(T=1/2) + d, X0(T=1/2)->&Lambda + n/&Sigma- + p----(IV):X0(T=1/2) dibaryon production and its &Lambda n/&Sigma- p decay,

are expected. Here, all FSI (elastic re-scattering, &Sigma&Lambda conversion) were not listed. Very unfortunately, all these processes cannot discriminated by purely kinematical consideration, and we do need some dynamics. For example, the relationship between dY invariant mass,MdY, and dY total 3-momentum, vec(ptotal)=vec(pd)+vec(pY), is as below:

(MYd)2 = (pY+pd)2 = (EY+Ed)2 - (vec(pY)+vec(pd))2=(Einit-EN)2 - |vec(ptotal)|2

=(Einit-sqrt(mN2+|vec(pN)|2))2 - |vec(ptotal)|2=(Einit-sqrt(mN2+|vec(ptotal)|2))2 - |vec(ptotal)|2

where the conservation of 4-momentum,

Einit=M4He+MK-=EY+EN+Ed,

vec(pinit)=vec(0)=vec(pY)+vec(pN)+vec(pd),

have been assumed.

Note that it is already known from YN correlation analysis that the process (I) does not produce a deuteron over 300 MeV/c, and it makes a broad peak at 3070 MeV/c^2 if the deuteron could be detected.

Event topologies

In order to examine them, we develop Yd correlation analysis here. The conditions are as follows:
  • The deuteron is preliminary identified by 1/&beta VS total energy on PB-NT.
  • The decay products of &Lambda/&Sigma- are detected by TC and PB-NT.
    • Hence, possible event topologies are limited within following two for each.

    Identification of &Lambda in coincidence with a deuteron

    As was already described, the &Lambda definition is Minv within (1108.,1124.)/(1111.,1121.)
    p&pi invariant mass spectra from case1(top)/case2(bottom) topological events. E549+E570 100% statistics are accumulated. The black is from all "deuteron" events, while the red/green are "signal"/"BG" events as described previously.
    p&pi invariant mass spectra from case1(top)/case2(bottom) topological events. E549+E570 100% statistics are accumulated. The black is from "signal" events. Among all events, the red is from the events in which the decay vertex is shifted toward the motion of &Lambda candidate, while the shift is the opposite side for the green.

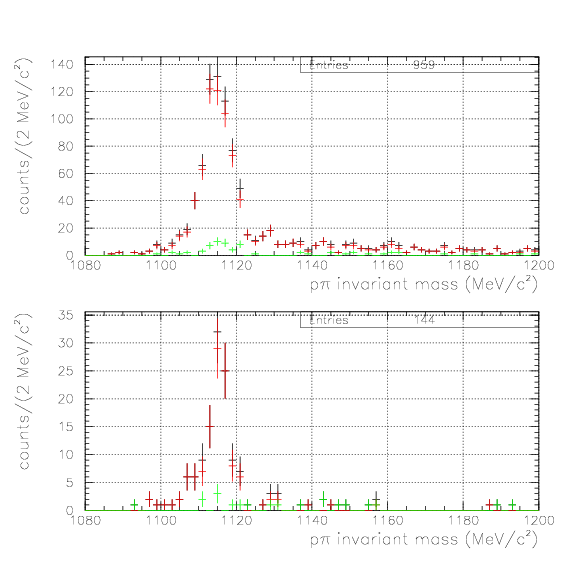
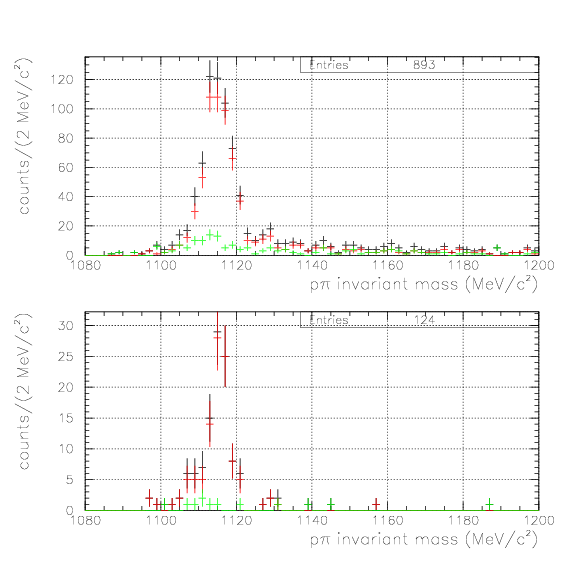
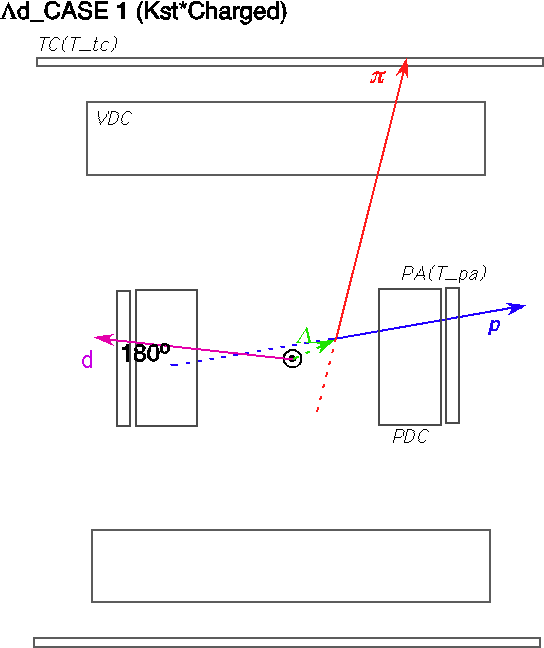
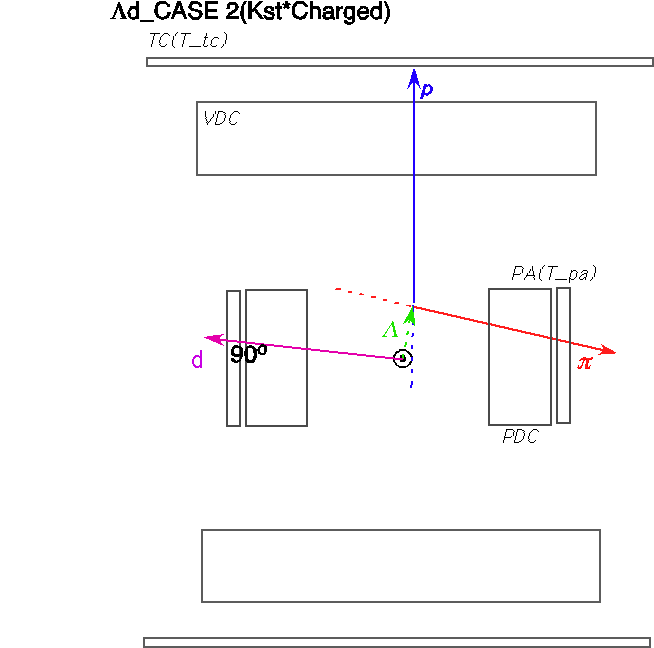
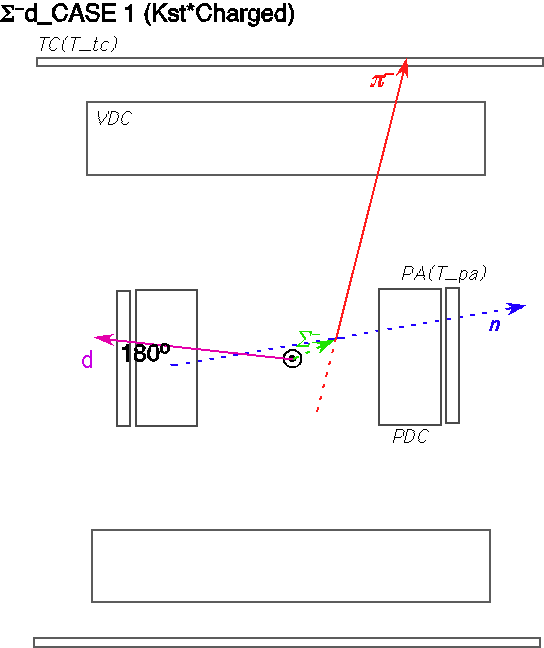
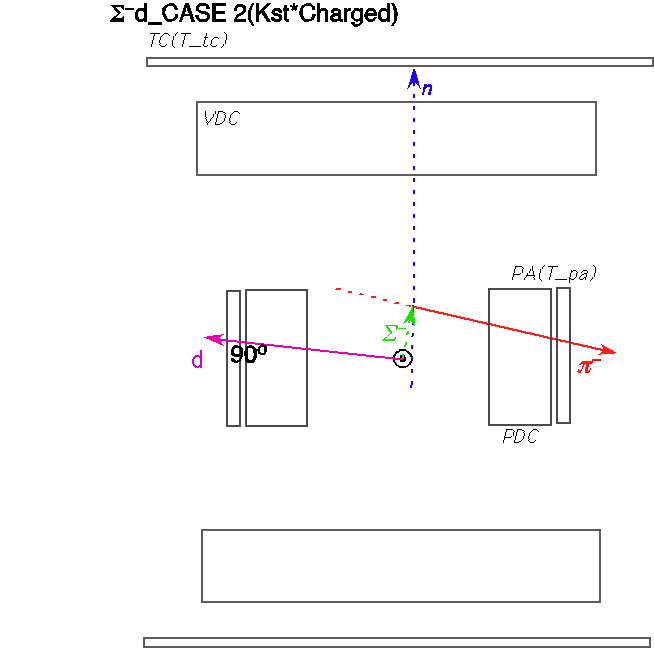
    To identify the &Lambda particle, we impose positive shift and p&pi invariant mass within (1108.,1124.)/(1111.,1121.) for case1/2, respectively.

    &Lambda d correlation

  • case1 result
  • case2 result

    • Identification of &Sigma- in coincidence with a deuteron

    As was already described in &Sigma-p sector, the &Sigma- definition is Minv within (1150.,1225.)/(1175.,1225.) for case 1/2. Of course, physical deuteron is selected, and neutron is selected by those giving energy deposit over 3 MeVee and 1.6 < 1/&beta < 9.0 in advance.
    n&pi invariant mass (top)/4He(stopped K-,dn)Y- mass (bottom) spectra from case1 topological events. E549+E570 100% statistics are accumulated. For the top, Red/green are used for VcaVn > 0./ < 0.,respectively. For the bottom, Y0 mass spectrum is divided into &Sigma-(magenta) and non-&Sigma-(sky-blue) events.
    n&pi invariant mass (top)/4He(stopped K-,dn)Y- mass (bottom) spectra from case2 topological events. E549+E570 100% statistics are accumulated. For the colored spectra, see the caption for the figure above.

    &Sigma^- d correlation

  • case1 result
  • case2 result

    • Translated Yd correlation

    In the dn/dp back-to-back coincidence spectrum, we have successfully reconstructed &Lambda0/&Sigma- hyperons. They do mean that we have identified the final states,

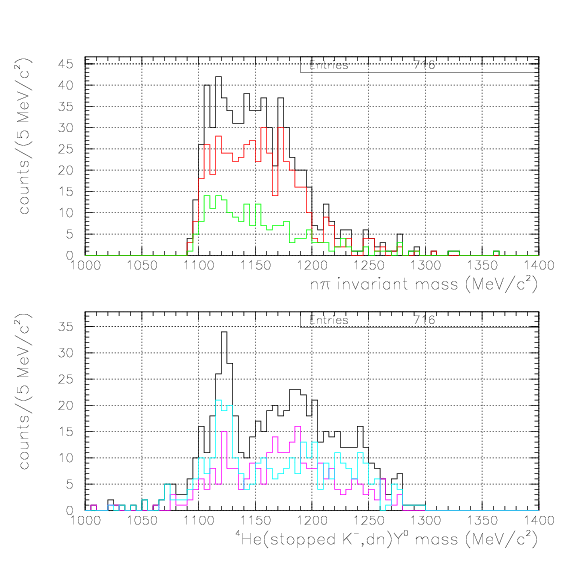
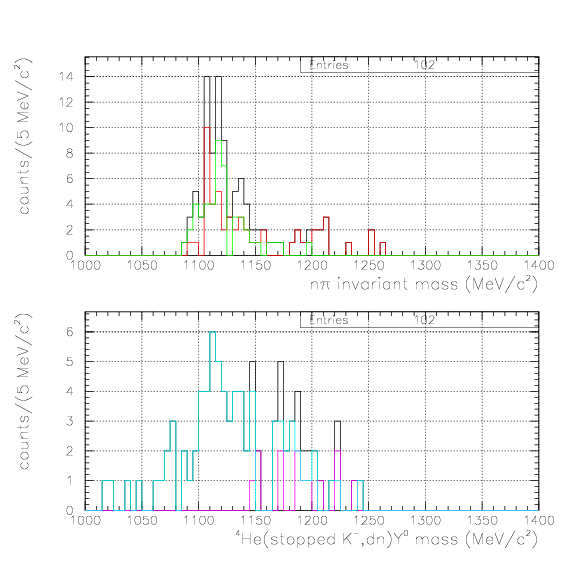
    K- + 4He -> &Lambda + n + d

    , and

    K- + 4He -> &Sigma- + p + d

    . The Y0/Y- mass spectra are shown below.

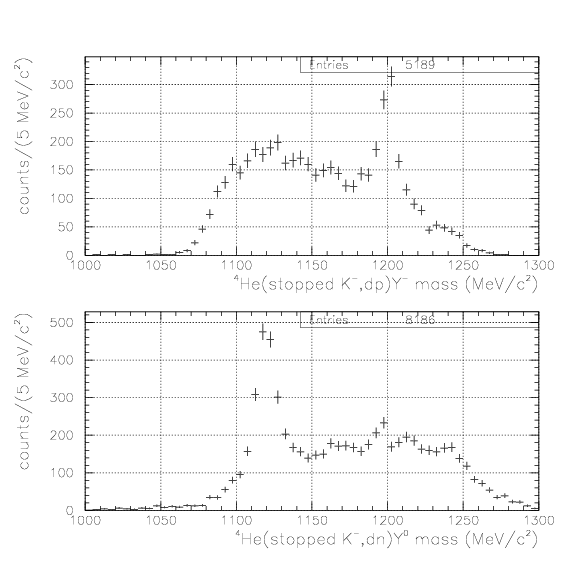
    The continuum of the Y0/- mass spectra originate from

    K- + 4He -> &Lambda + n + d->(p+&pi-) + n + d/(n+&pi0) + n + d

    , and

    K- + 4He -> &Sigma- + p + d -> (n + &pi-) + p + d

    . Then, it is possible to introduce hyperon 3-momentum pY(1:3) and Mmiss being defined by

    vec(pY)=-(vec(pd)+vec(pN)),

    Mmiss=sqrt((M4He+MK--EN)2-PN2)

    , and treat them as hyperon 3-momentum and Yd invariant mass. The &Lambda/&Sigma- are defined adequately after investigation of S/N ratio.
  • &Lambda d result from dn back-to-back events
  • &Sigma- d result from dp back-to-back events

    • Acceptance-uncorrected Dalitz Plots of the YdN final states

    A Dalitz plot of a &Lambda d n final state. The case1/case2/compiled results are exhibitted with red/green/black.
    A Dalitz plot of a &Sigma- d p final state. The case1/case2/compiled results are exhibitted with red/green/black.