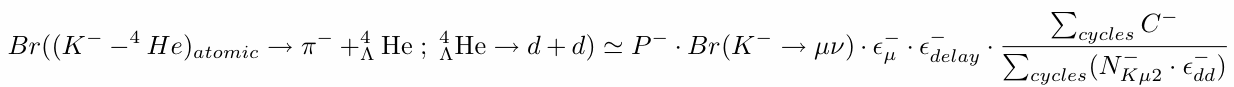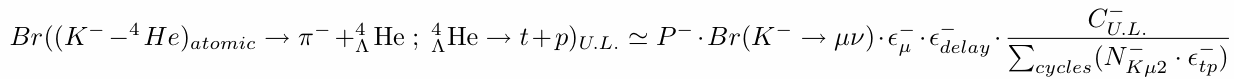Particle/Nuclear Mass table
| software | GEANT3.21(partice tracking tuned for slow particles) |
| Formation reaction | (K--4He)atomic -> 4&LambdaHe + &pi- (254.6 MeV/c with 4&LambdaHe mass shown below), 100% |
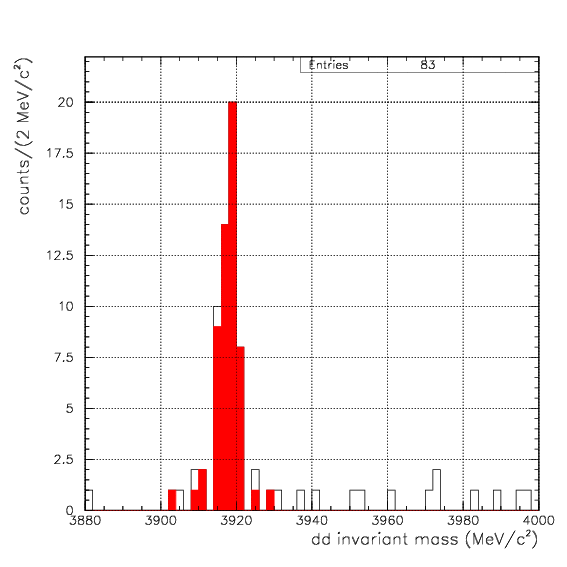
| 4&LambdaHe mass | M3He(2809.23)+M&Lambda(1115.684)-2.39 = 3922.5 (MeV/c2) |
| 4&LambdaHe decay modes/bracnhing ratio on the simulation | d+d:t+p:3He+n=40%(573.2MeV/c):40%(509.1MeV/c):20%(507.4MeV/c) |
| 4&LambdaHe Life time | 257 psec : figure / 250 +- 18 psec : acceptance |
| (K--4He)atomic life time | 6.6*10-17 sec (Γ=10 eV) |
| Generated number of (K--4He)atomic / 4&LambdaHe | 2*107 |
| Target center | (-0.3,0.,1.3):E549 (-0.5,0.5,1.2):E570 |
| x/y generation point distribution | 4.0 cm &sigma Gaussian centered at (x,y)=(-0.3,0.) |
| z generation point distribution | uniform |
| Multiple scattering | on(Moliere) |
| Energy loss straggling | on(Gauss/Landau/Vavilov are internally selected adequately) |
| In-flight nuclear reaction of p/d | on(GHEISHA, unique selection for in-flight reaction loss for d) |
| Coincidense time gate for PA-PB | 45 nsec |
| Birk's coefficients | 0.013/(MeV/cm), 9.6E-06/(MeV/cm)2 for PA/PB/NT |
| Time resolution of PA/PB | 60/90 psec (~108.2 psec in total), fixed at MIP-measured value. |
| Proton/Deuteron selection | Simulated with 1/&beta VS total Light output (with infinite energy resolution). |
| PDC hit | Only 1 particle is accepted per chamber. Multi track events (p+&pi-,etc) are eliminated. |
| Inefficiency of energy loss correction | Newly considered. As the reaction vertex, exact position is adopted. The direction vector at the PDC position is adopted as the direction vector to simulate properly the experimental effect. |
Properties of the process
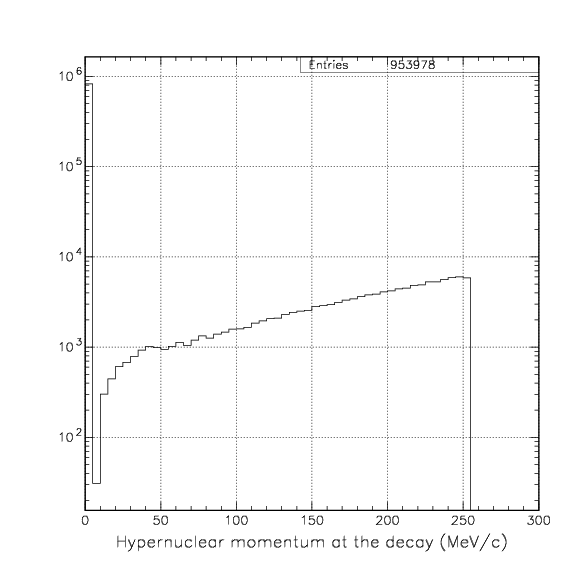
Momentum distribution of 4&LambdaHe at the decay. ~86.4% decay at rest.
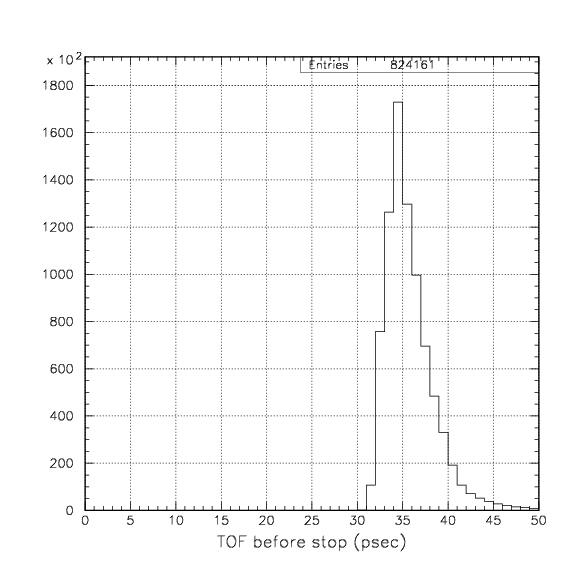
TOF of 4&LambdaHe until stopping if they decay at rest.
Range spectrum of 4&LambdaHe. Its tipical range is ~0.5 mm in 4He.
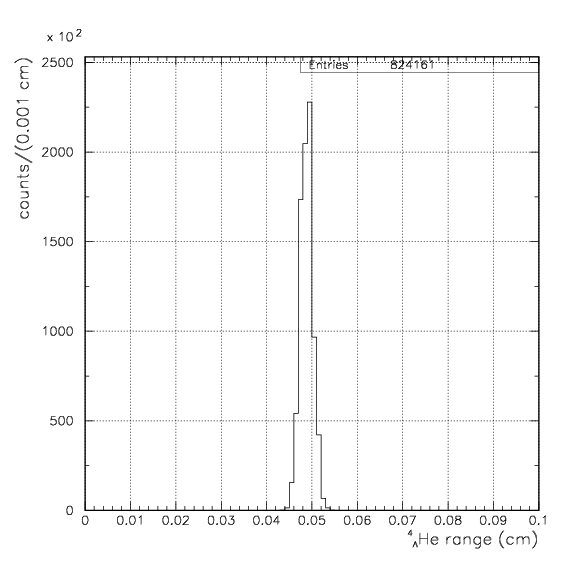
Decay timing spectrum. The decay timing is defined as the time difference between the formation of K--4He atom and the decay of 4&LambdaHe regardless the status (in-flight or at rest) at the decay. The lifetime is found to be 257 psec by the fitting of an exponential function.
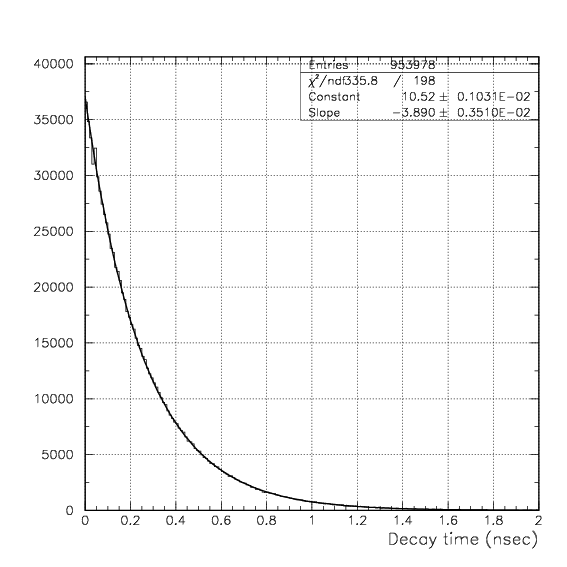
Range spectra for 3H and 3He in super-fluid 4He. Tritons can fire the PA, but 3He cannot.
Results
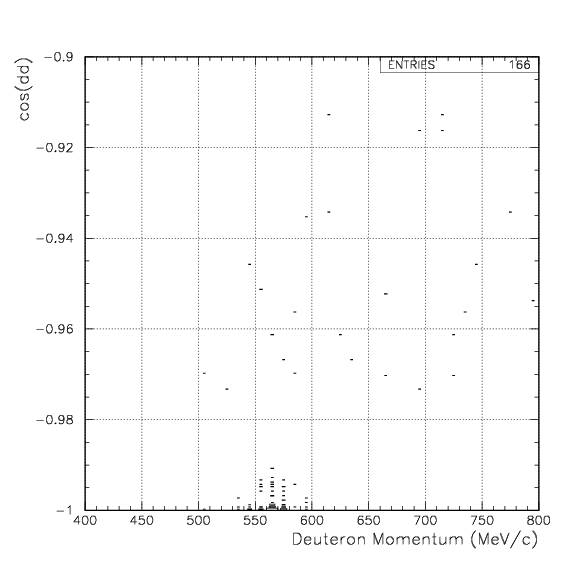
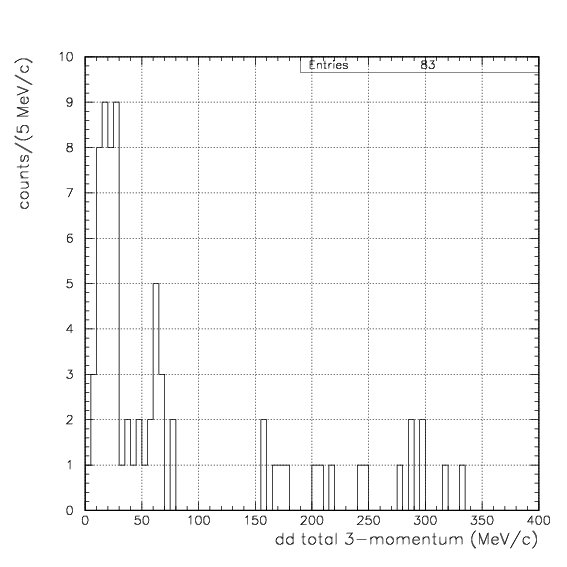
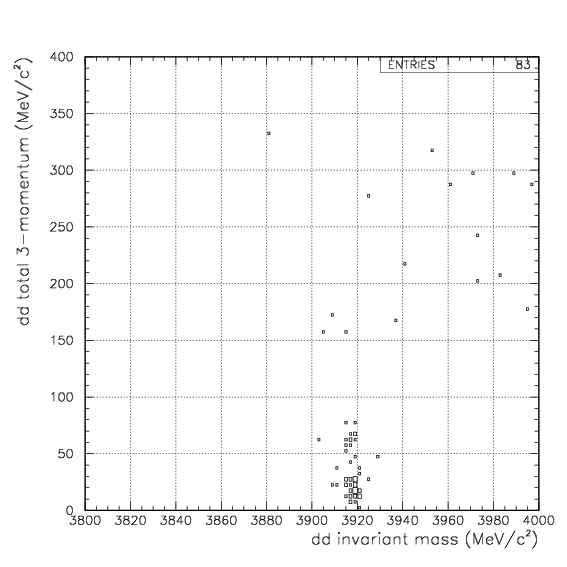
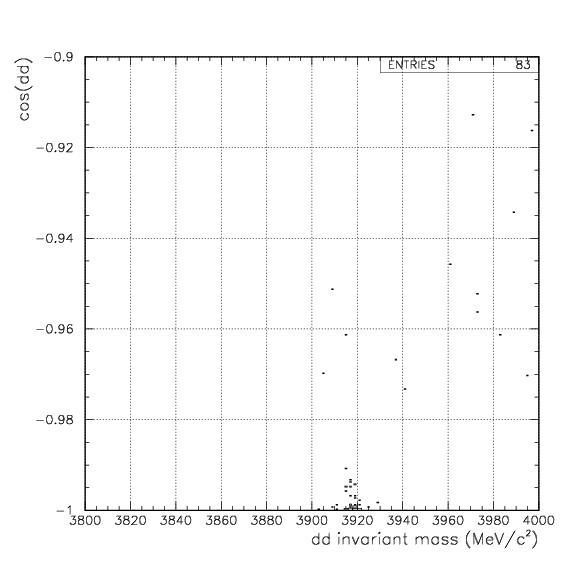
As already shown, d+d decay channel was observed by back-to-back coincidence of dd pair. As expected from the range spectrum, p+t channel would be barely seen with the triton stops on PA leaving a charged particle track on PDC, in coincidence with a proton with 508 MeV/c momentum detected on the opposite arm. Therefore, we try to evaluate the physical acceptance of ....1. dd events - back-to-back dd coincidence on PDC/PA/PB,
2. pt events - p on PDC/PA/PB and t on PDC/PA on the opossite arm.
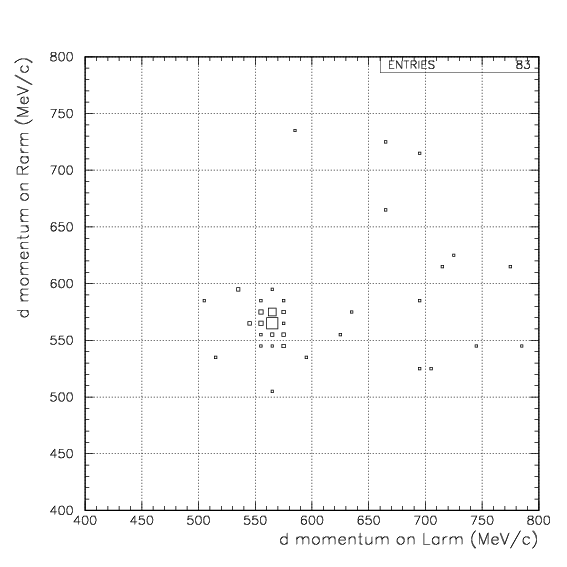
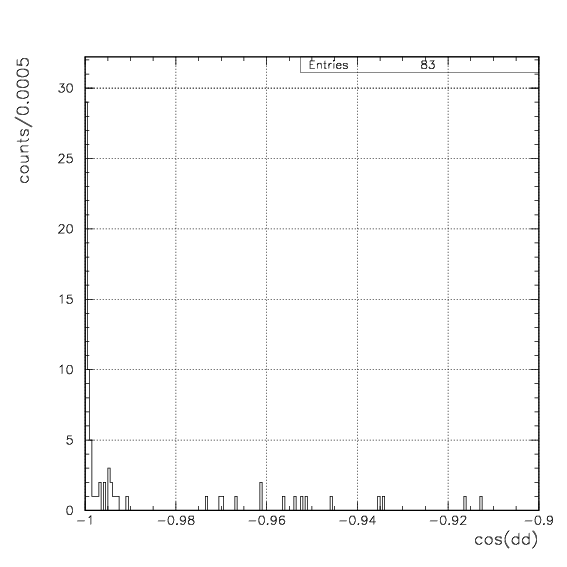
In these conditions, simuated decay vertex and cos(dd/pt) distributions with the geometrical bias are exhibited below. The red spectra are from stopped 4&LambdaHe decay, while the blue are from in-flight events.Simulated decay vertex and cos(dd) distribution for dd events. Event selection procedure of deuteron is applied on both arm as done for data.
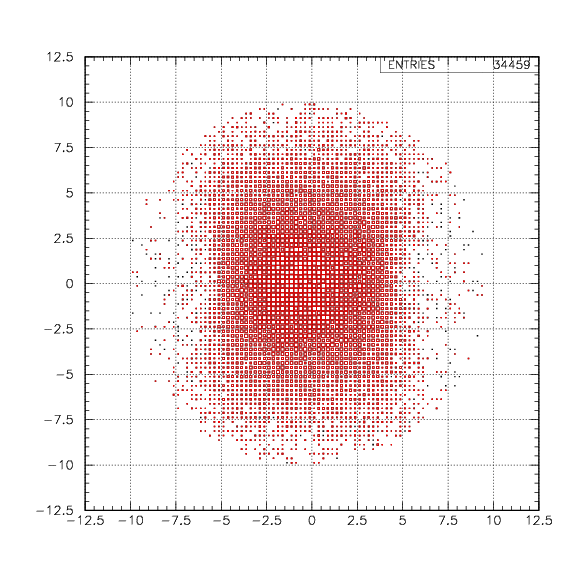
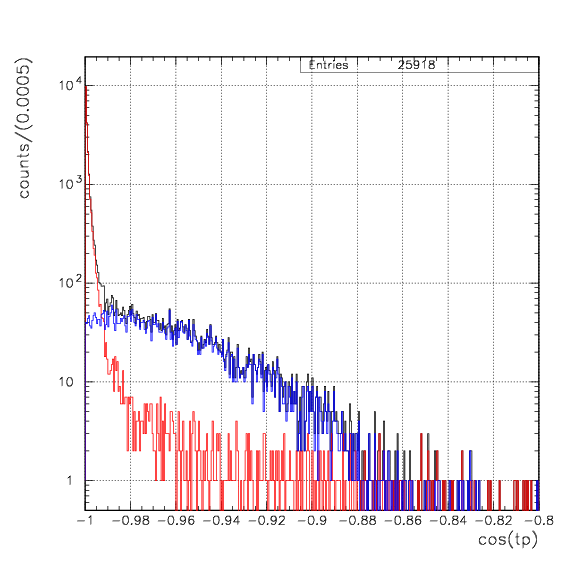
Simulated decay vertex and cos(pt) distribution for pt events. proton slection procedure is applied as done for data, and t on PA is required on the opposite arm.
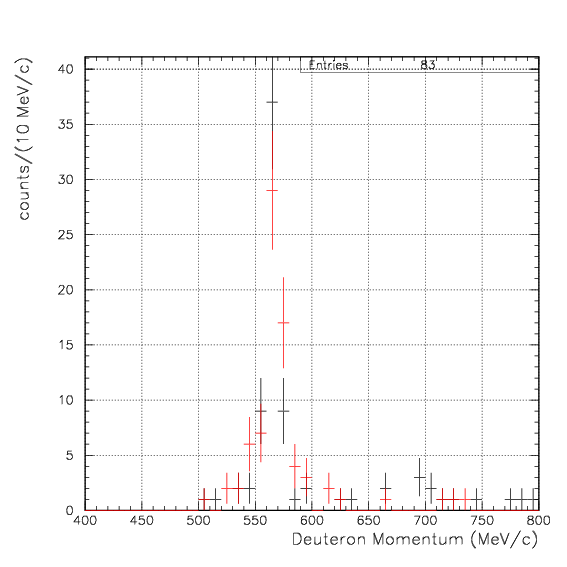
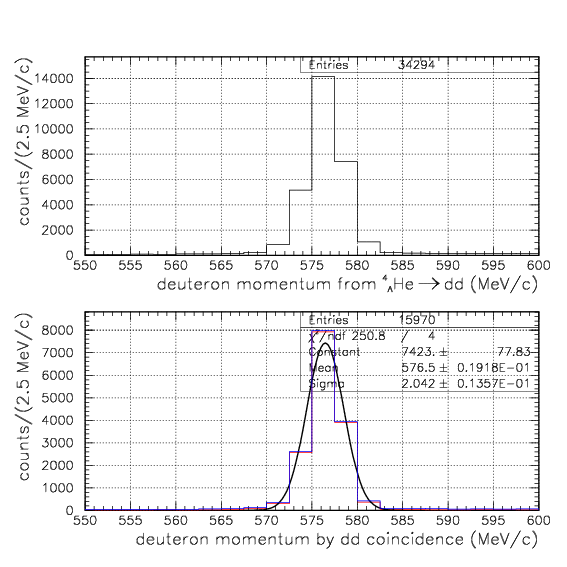
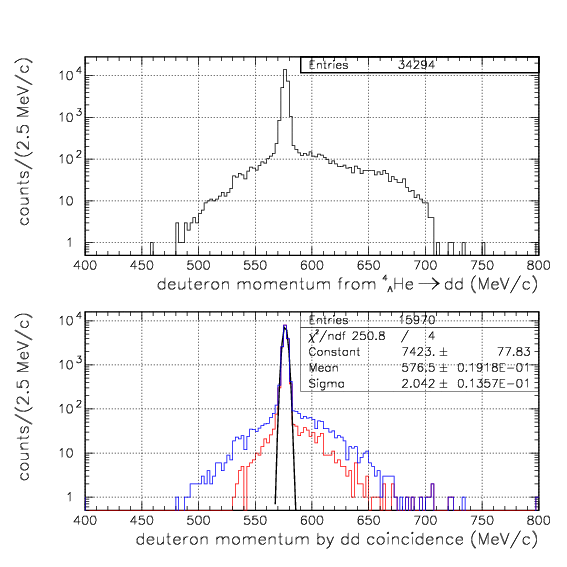
Simulated deuteron momentum distribution by 4&LambdaHe->dd events on the left arm. The top is constructed from the event set if a deuteron is detected and identified with successfull energy loss correction on the left arm. In the bottom, we further require detection and identification of another d in the counter-PDC-PA-PB R arm, which directly corresponds to the measured momentum spectrum presented above. The blue shows the whole events, while the red shows the events from stopped 4&LambdaHe decay. The Gaussian fitting to the bottom-red gives ~2.0 MeV/c as the standard deviation. Linear-scale and log-scale figures are presented simultaneously.
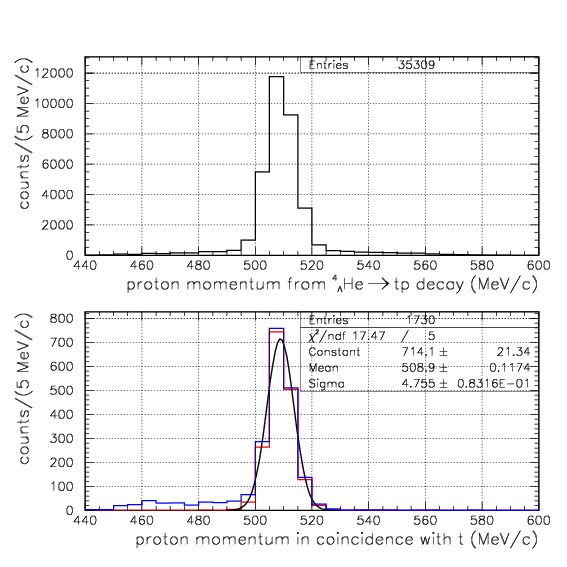
Simulated proton momentum distribution by 4&LambdaHe->tp events. The top is constructed from the event set if a proton is detected and identified with successfull energy loss correction. In the bottom, we further require detection of t in the counter-PDC-PA arm. The blue shows the whole events, while the red shows the events from stopped 4&LambdaHe decay. The Gaussian fitting to the bottom-red gives ~4.8 MeV/c as the standard deviation.
The step-by-step evaluation of &epsilondd and &epsilontp are tabulatted below:
| Cycle | Life time (psec) | generated event No. of dd decay | PDC-PA-PB hit of d | PDC-PA-PB hit of another d | time gate (45 nsec) + d selection on analysis (double) | Successful energy loss correction (double) | cos(dd)<-0.99 | &epsilondd (%) |
|---|---|---|---|---|---|---|---|---|
| E549 | 232 | 7.63051E+06 | 650304(550444) | 223544(205111) | 203434(187051) | 199988(184042) | 187403(183630) | 2.456 |
| E549 | 250 | 7.63429E+06 | 649406(555910) | 225301(208034) | 205168(189755) | 201741(186720) | 189958(186321) | 2.488 |
| E549 | 257 | 7.63669E+06 | 650645(559749) | 226593(209722) | 206411(191409) | 202952(188355) | 191319(187908) | 2.505 |
| E549 | 268 | 7.63644E+06 | 649973(562708) | 226281(210275) | 206050(191827) | 202674(188834) | 191725(188394) | 2.511 |
| E570 | 232 | 7.58286E+06 | 636601(539080) | 209310(192650) | 188505(173821) | 184781(170521) | 173353(170015) | 2.286 |
| E570 | 250 | 7.57735E+06 | 636998(545510) | 210741(195079) | 189808(176021) | 186048(172703) | 175394(172151) | 2.315 |
| E570 | 257 | 7.57948E+06 | 637705(548961) | 211302(196179) | 190181(176847) | 186521(173576) | 176151(173030) | 2.324 |
| E570 | 268 | 7.58212E+06 | 637878(552292) | 212166(197620) | 190785(177932) | 187117(174631) | 177065(174052) | 2.335 |
| Cycle | Life time (psec) | generated event No of tp decay. | PDC-PA-PB hit of p | PDC-PA hit of t | time gate (45 nsec) + selection on analysis (p only) | Successful energy loss correction (p only) | cos(tp)<-0.99 | &epsilontp(%) |
|---|---|---|---|---|---|---|---|---|
| E549 | 232 | 7.63546E+06 | 535167(454178) | 30259(23249) | 26244(20201) | 26036(20045) | 20373(19431) | 2.545E-01 |
| E549 | 250 | 7.63493E+06 | 533210(458144) | 29737(23419) | 25772(20382) | 25588(20233) | 20461(19621) | 2.570E-01 |
| E549 | 257 | 7.63293E+06 | 533087(459672) | 29730(23434) | 25817(20380) | 25620(20228) | 20504(19649) | 2.574E-01 |
| E549 | 268 | 7.63342E+06 | 533432(462909) | 29822(23819) | 25821(20692) | 25631(20538) | 20746(19948) | 2.613E-01 |
| E570 | 232 | 7.58012E+06 | 530726(450900) | 21837(16140) | 18944(14024) | 18767(13899) | 14136(13427) | 1.771E-01 |
| E570 | 250 | 7.57949E+06 | 529807(454815) | 22146(16667) | 19355(14609) | 19175(14470) | 14699(13979) | 1.844E-01 |
| E570 | 257 | 7.58236E+06 | 530861(458013) | 21583(16400) | 18644(14199) | 18475(14074) | 14210(13600) | 1.794E-01 |
| E570 | 268 | 7.57706E+06 | 529216(459550) | 21810(16708) | 19044(14650) | 18858(14510) | 14699(14014) | 1.850E-01 |
Finalized per-stopped-K- branching ratio of dd mode
Substituting all numerical values, we finally obtain the per-stopped-K- branching fraction of the hyper-nuclear cascade reaction,(4He-K-)atomic-> &pi-+4&LambdaHe,
4&LambdaHe-> d+d,
asBr((4He-K-)atomic-> &pi-+4&LambdaHe ; 4&LambdaHe -> d+d)=1.34±0.19(syst)±0.18(stat)×10-5 (per stopped K-).
As the source of the systematic error, we considered only the error attributed to the free-decay rate of K- in meta-stable orbits. Relative error attributed to the quantitiy is more than one order larger than other possible sources, and hence the simple estimation is obviously justified.