Today's Progress 20. June. 2007

Deuteron spectra/Yd correlation analysis (1)

Identification of deuterons

Enlarged cycle-by-cycle arm-by-arm correlations between 1/&beta and total light output are shown below. The proton component is eliminated to make deuteron component more clear on the plot. The deuteron component appears around 1/&beta 2.8~8.0. The triton component is barely seen.

The deuteron ID function is defined cycle-by-cycle arm-by-arm as done for proton. A 6 order polinomial (7 parameters) is adopted to fit the light output as the function of 1/&beta globally.

Then, deuteron ID function is defined as

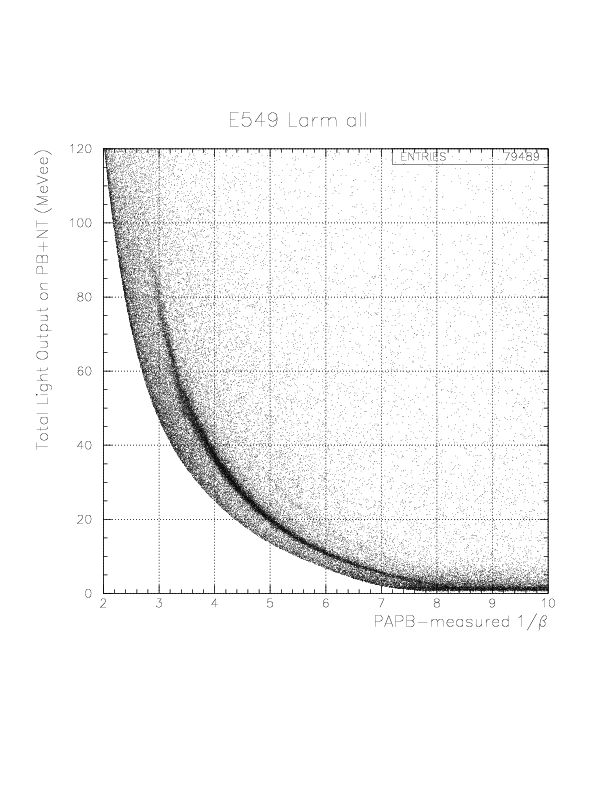
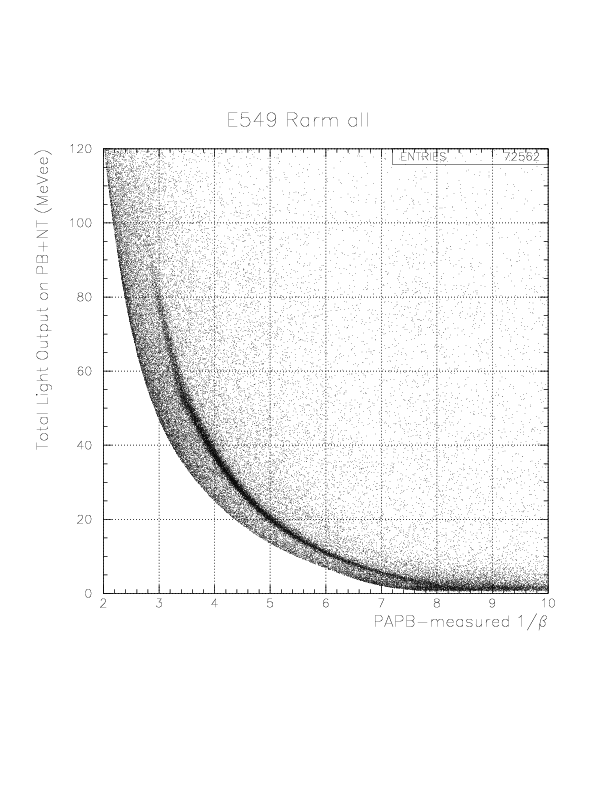
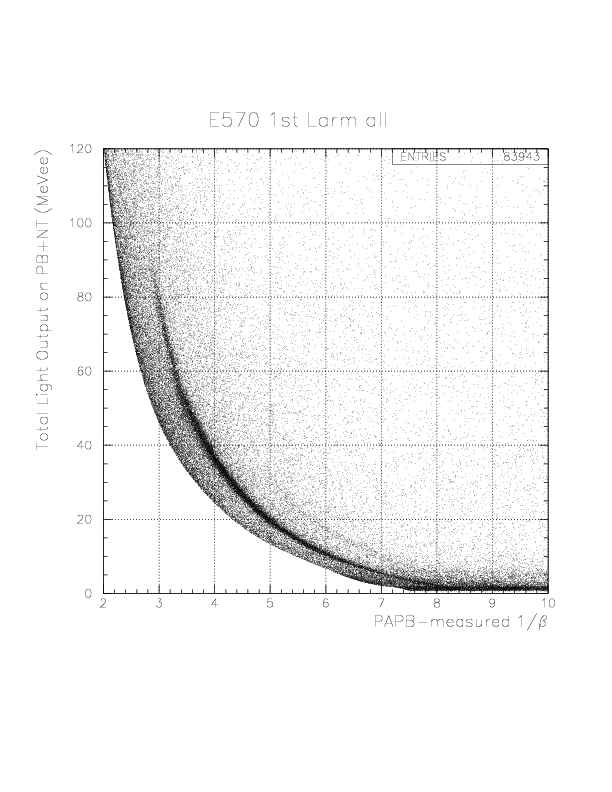
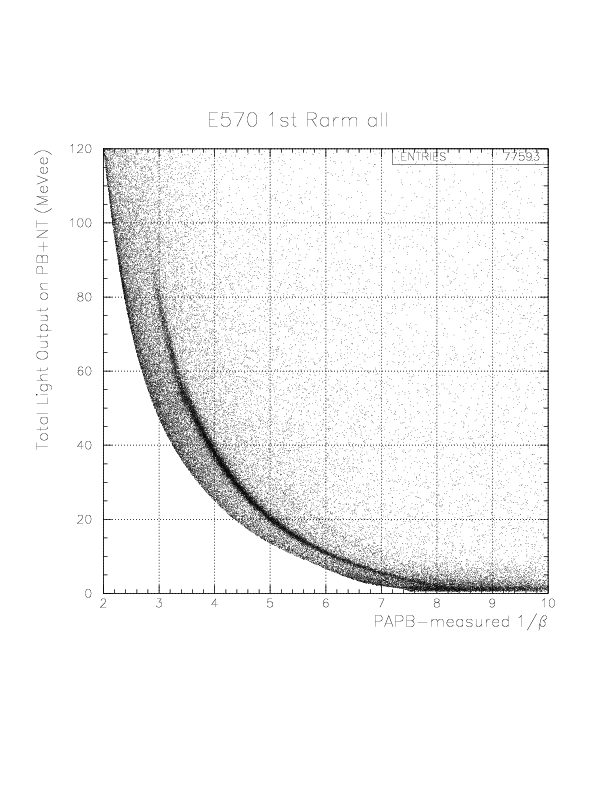
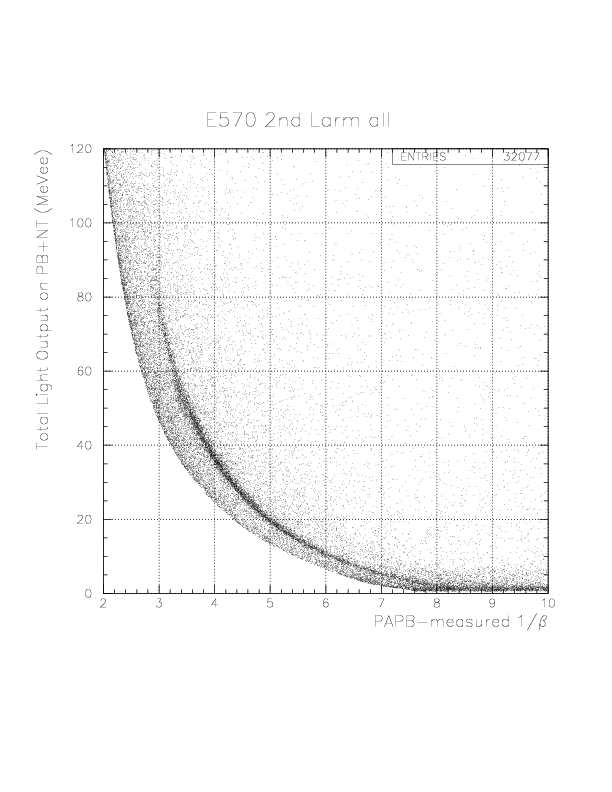
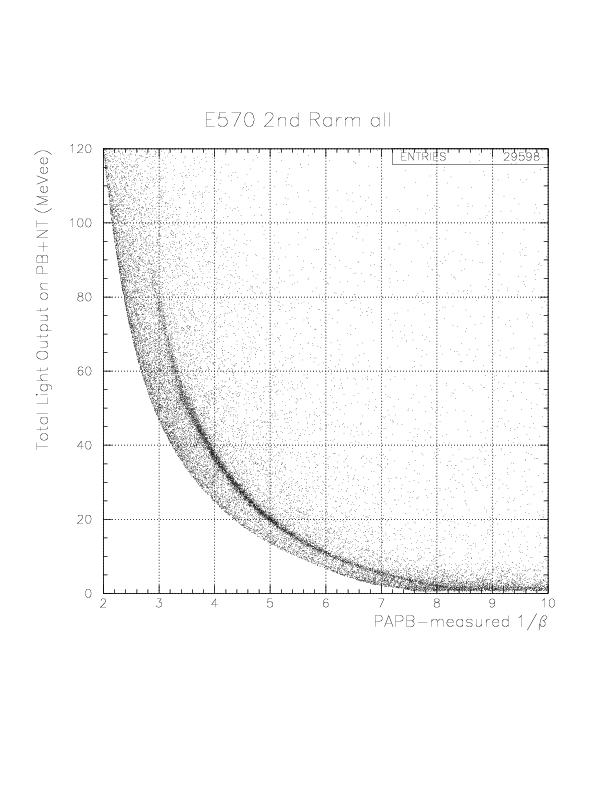
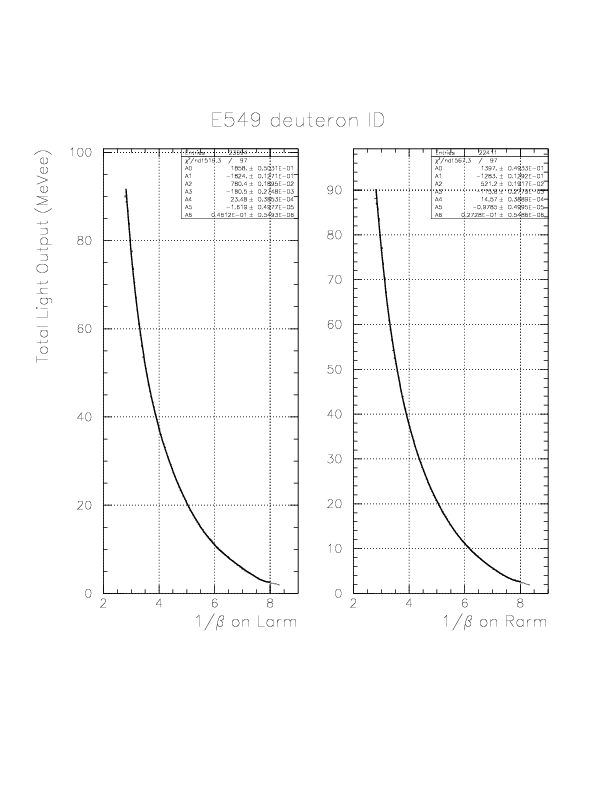
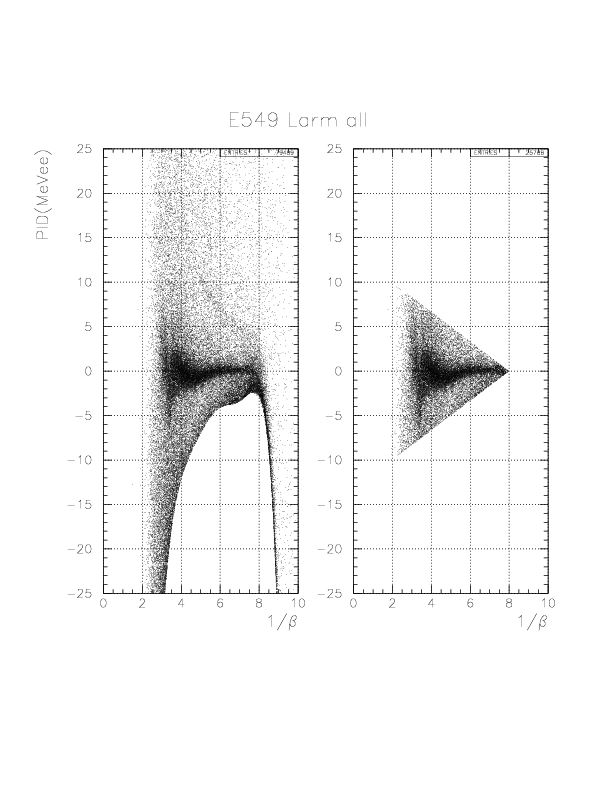
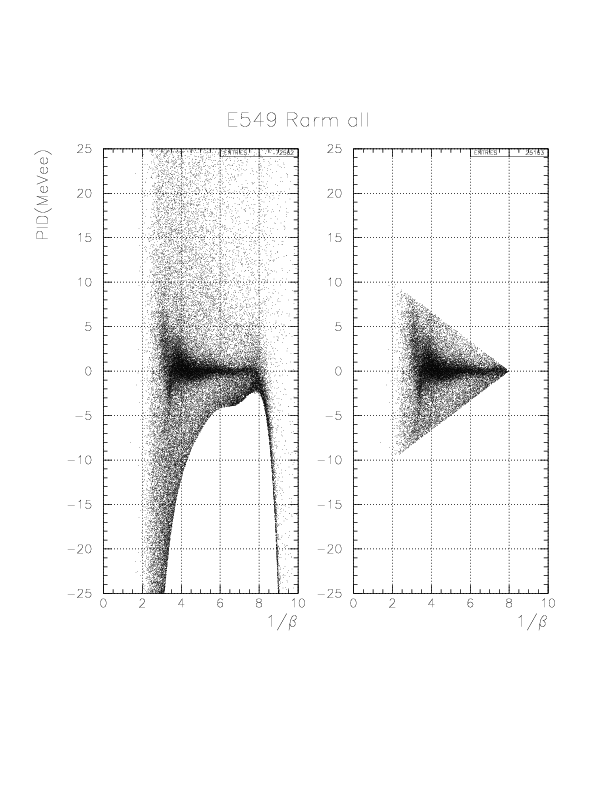
PID= T.E(PB/NT) - f(1/&beta(PA-PB)) (MeVee).

In order to select the 'deuteron' by 1/&beta-dependent way, we introduce a phenomenological function, g(1/&beta) as the straight line passing through two points (1/&beta, PID) = (8.0, 0.),(2.0, 10.),

g(1/&beta) -0.0= (0.0-10.0)/(8.0-2.0)*(1/&beta-8.0).

Then, we define the 'deuteron' events by the condition,

|PID| < g(1/&beta).

PID vs 1/&beta . Deuterons are selected at 2.8~8.0 1/&beta region.

⁴He(stopped K^-,d) inclusive/coincidence spectrum

Cycle-by-cycle arm-by-arm deuteron 1/&beta spectra are shown below.

1/&beta spectra of deuteron.

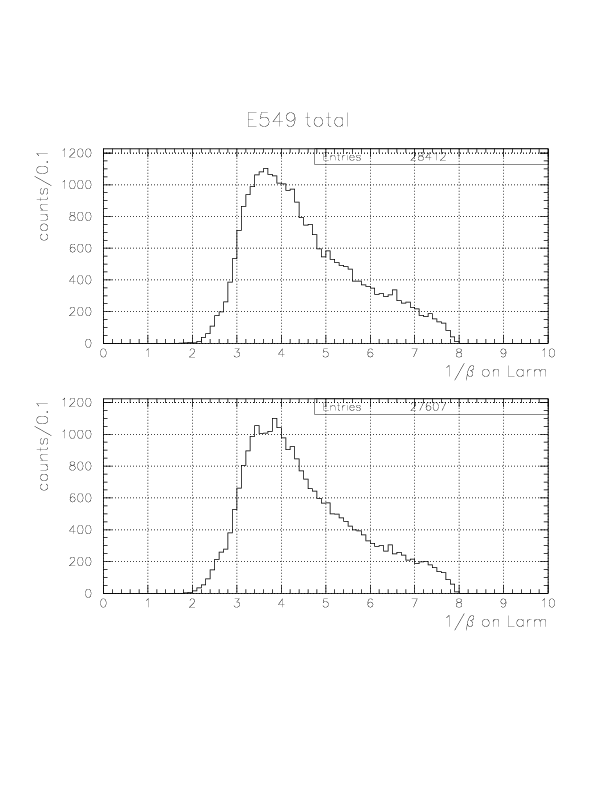
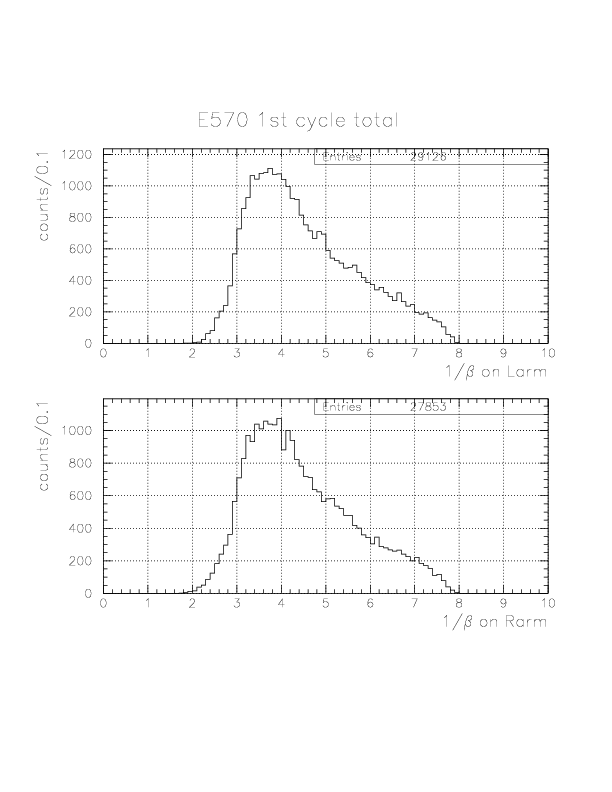
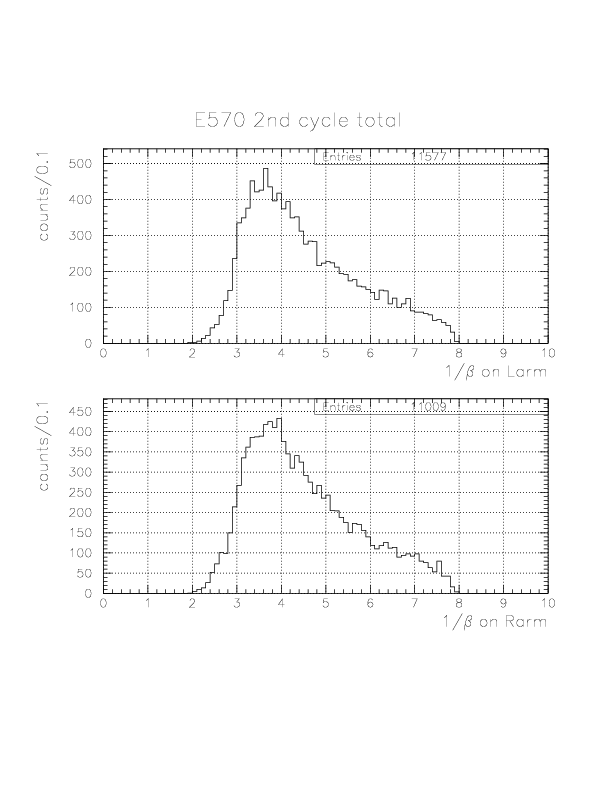Inclusive spectra

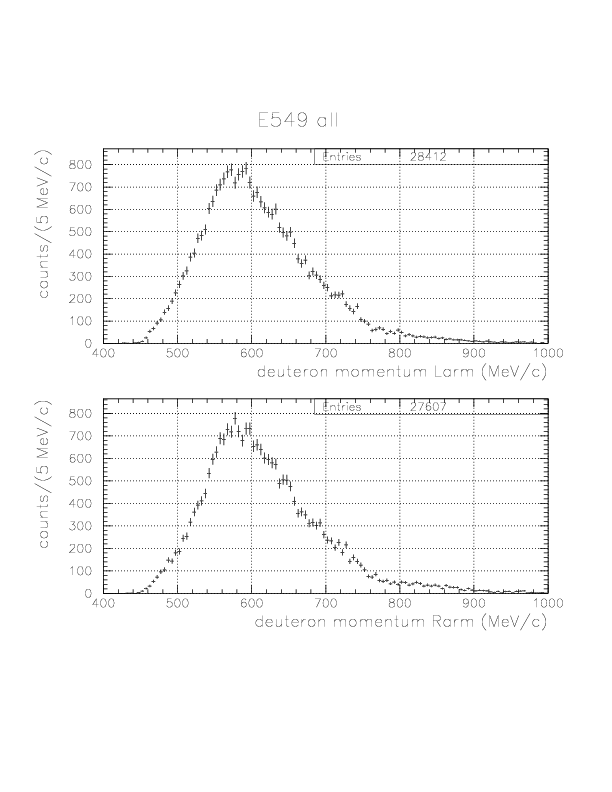
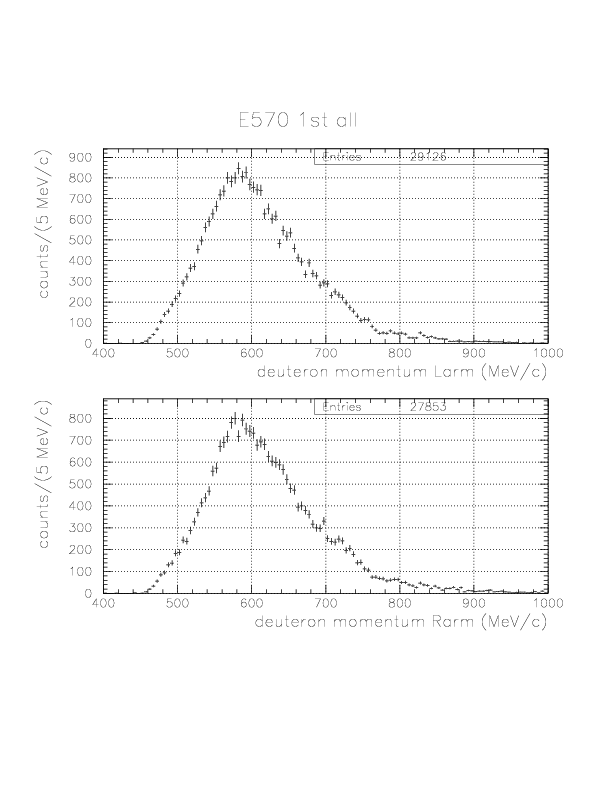
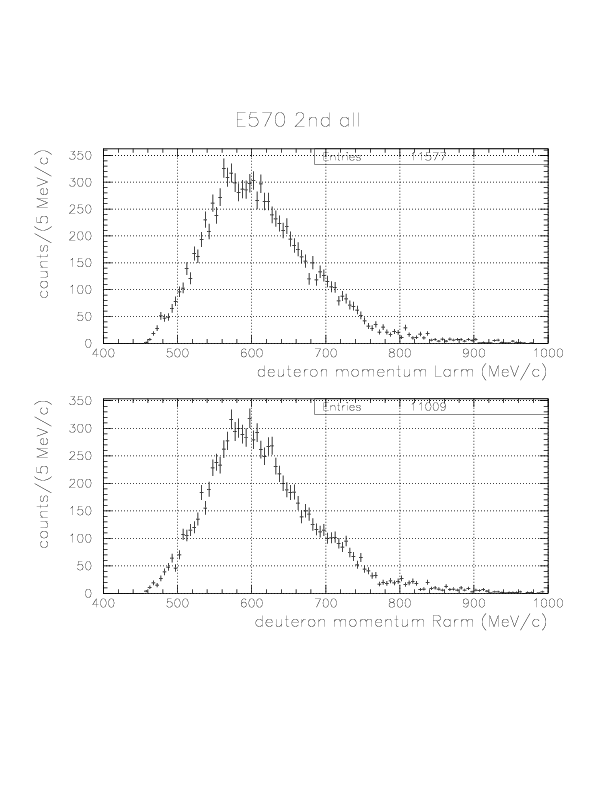
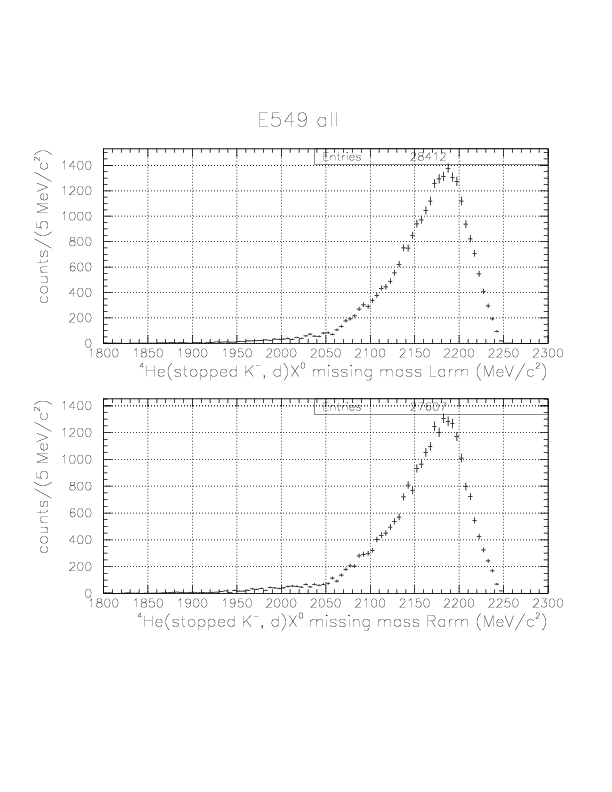
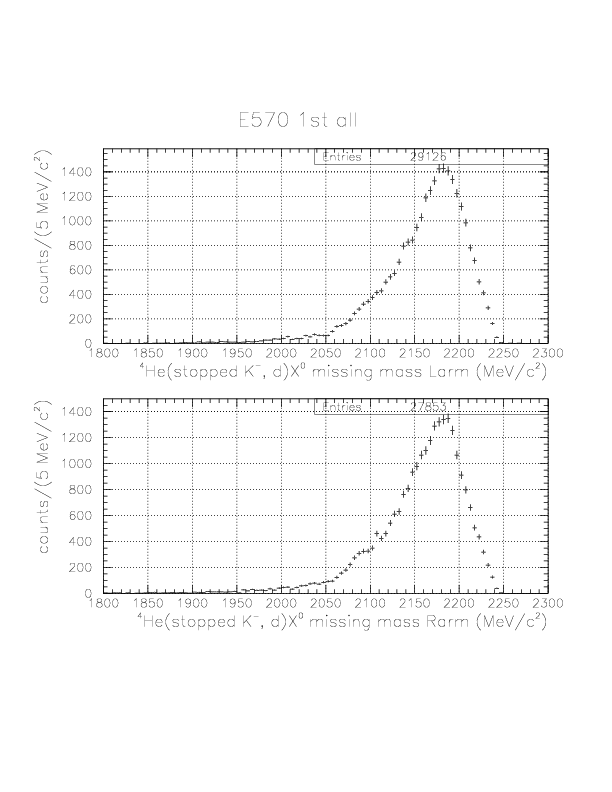
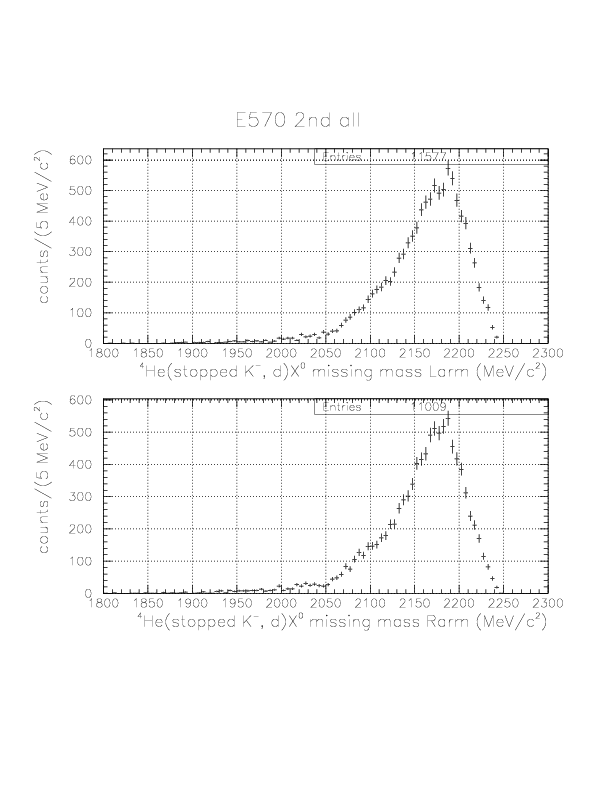
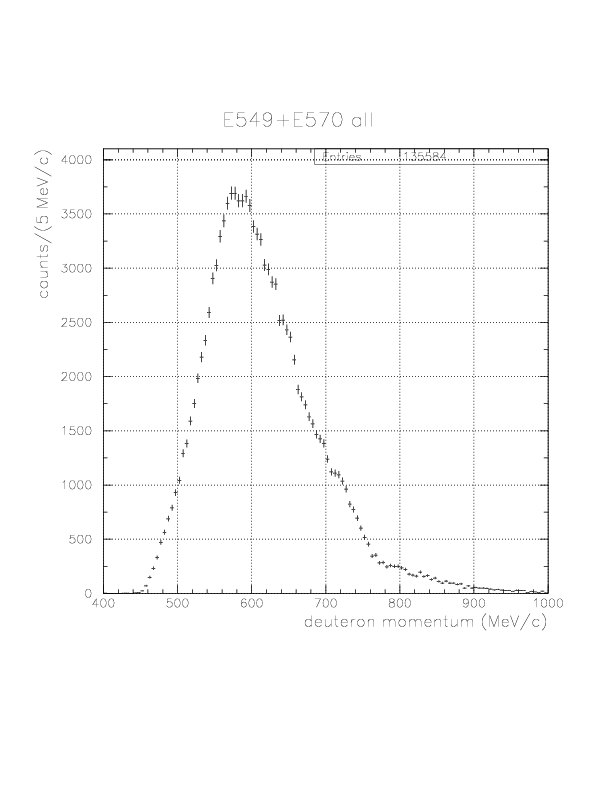
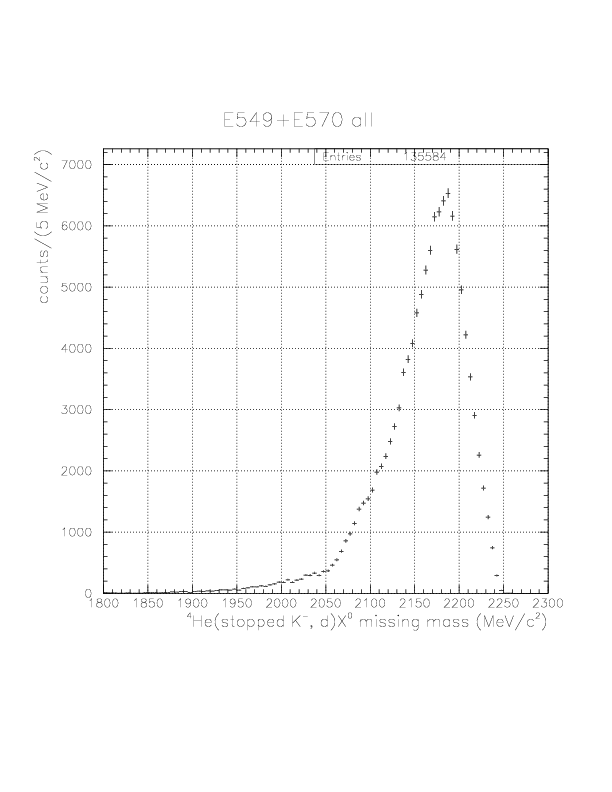
Deuteron inclusive momentum/⁴He(stopped K^-, d)X⁰ missing mass spectra are shown below. In principle, they can be normalized to "percent of stopped K^-" unit as was done for proton. Physical limits of the momentum/missing mass are ~760 MeV/c / 2055 MeV/c², and we see non-negligible high-momentum background due to particle miss-identification.

Cycle-by-cycle deuteron momentum spactra.

Cycle-by-cycle missing mass spectra.

Inclusive spectra with full statistics

Coincidence spectra

Below, deuteron spectra are presented under various coincidence conditions. The conditions are:

1. &pi on TC

2. p on TC

3. n(3MeVee) on TC

4. &pi on NT (d-&pi back-to-back)

5. p on NT (d-p back-to-back)

6. n(3MeVee) on NT (d-n back-to-back)

Variable definition is as follows:

deuteron 4-momentum p_d(0:3)/3-momentum p'_d(3):p_d(i)=p'_d(i) (i=1,2,3), p_d(0)=sqrt(M_d²+|p'_d|²),

Nucleon 4-momentum p_N(0:3)/3-momentum p'_N(3):p_N(i)=p'_N(i) (i=1,2,3), p_N(0)=sqrt(M_N²+|p'_N²|)

cos(Nd):p'_d*p'_N/(|p'_d|*|p'_N|)

Nd total 3-momentum P_tot:sqrt((p_d(1)+p_N(1))²+(p_d(2)+p_N(2))²+(p_d(3)+p_N(3))²)

Nd total energy E_tot:p_d(0)+p_N(0)

⁴He(stopped K^-,Nd)Y^-/0 missing mass M_miss:sqrt((M_⁴He+M_K^--E_tot)²-P_tot²)

d&Lambda correlation - principle

By using &Lambda d pair detected simultaneously, we can study the final state

K^- + ⁴He -> &Lambda + n + d.

Even if we detect &Lambda and d simultaneously, the final state can be contaminated by

K^- + ⁴He -> &Lambda + p + &pi^- + d,

K^- + ⁴He -> &Lambda + n + &pi⁰ + d,

K^- + ⁴He -> &Sigma⁰(&Lambda&gamma) + n + d,

K^- + ⁴He -> &Sigma⁰(&Lambda&gamma) + p + &pi^- + d,

K^- + ⁴He -> &Sigma⁰(&Lambda&gamma) + n + &pi⁰ + d.

The pionic final states are very difficult to be detected due to the small reaction Q-values. All of the contaminants can be eliminated by imposing ⁴He(stopped K^-, d&Lambda)X missing mass being neutron mass.

This final state is considered to include possible 3 subcomponents, as

K^- + "pn" -> &Lambda + n + d (1:"2"-nucleon absorption &Lambda n d branch),

K^- + ⁴He -> S⁺ + n, S⁺->&Lambda + d (2:S⁺ tribaryon production and its &Lambda d decay),

K^- + ⁴He -> X⁰ + d, X⁰->&Lambda + n (3:X⁰ dibaryon production and its &Lambda n decay).

Very unfortunately, they cannot discriminated by purely kinematical consideration, and we do need some dynamics. For example, the relationship between d&Lambda invariant mass,M_d&Lambda, and d&Lambda total 3-momentum, vec(p_total)=vec(p_d)+vec(p_&Lambda), is as below:

(M_d&Lambda)² = (p_d+p_&Lambda)² = (E_d+E_&Lambda)² - (vec(p_d)+vec(p_&Lambda))²=(E_init-E_n)² - |vec(p_total)|²

where the conservation of 4-momentum,

E_init=M_⁴He+M_K^-=E_d+E_n+E_&Lambda,

vec(p_init)=vec(0)=vec(p_d)+vec(p_n)+vec(p_&Lambda),

have been assumed.

Note that it is already known from &Lambda n correlation analysis that the process 1 does not produce a deuteron over 300 MeV/c, and it makes a broad peak at 3070 MeV/c^2 if the deuteron could be detected.

Event topologies

In order to examine them, we develop &Lambda d correlation analysis here. The conditions are as follows:

The deuteron is identified by 1/&beta VS total energy on PB-NT.

The decay products of &Lambda are detected by TC and PB-NT.

Hence, possible event topology is limited within following two.

Identification of &Lambda in coincidence with a deuteron

As was already described, the &Lambda definition is Minv within (1108.,1124.)/(1111.,1121.)

p&pi invariant mass spectra from case1(top)/case2(bottom) topological events. E549+E570 100% statistics are accumulated. The red is TOF/energy correction with reaction vertex, while the black is TOF/energy correction with decay vertex.

p&pi invariant mass spectra from case1(top)/case2(bottom) topological events. E549+E570 100% statistics are accumulated. The red is when the decay vertex is shifted towards the motion of &Lambda candidate, while the shit is toward the opposite side for the green.

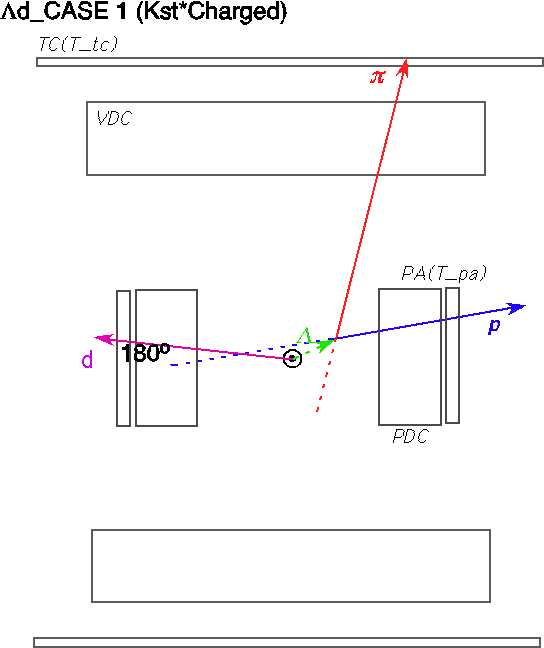
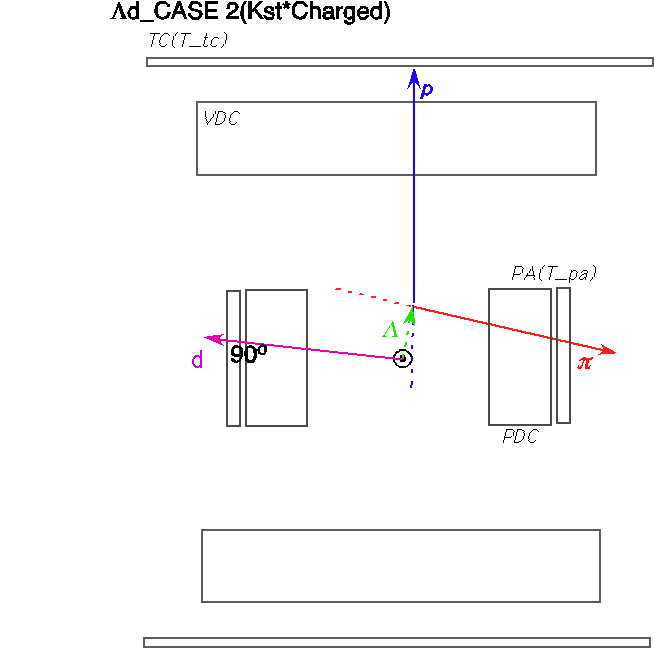
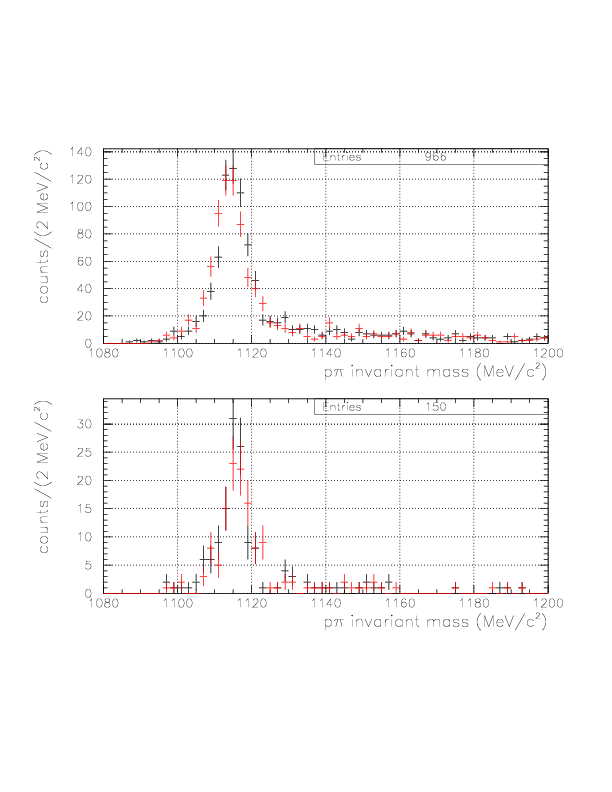
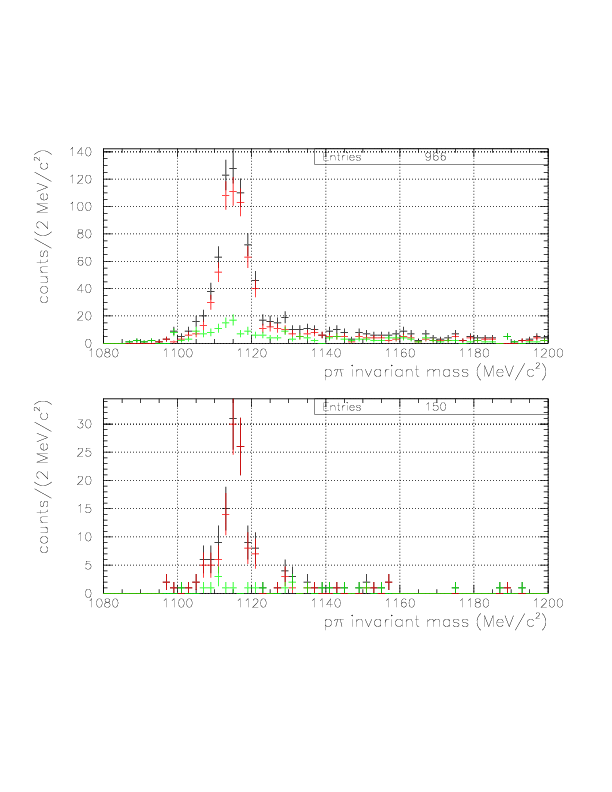
To identify the &Lambda particle, we impose positive shift and p&pi invariant mass within (1108.,1124.)/(1111.,1121.) for case1/2, respectively.

&Lambda d correlation

case1 result

case2 result

Translated Yd correlation

In the dn/dp back-to-back coincidence spectrum, we have successfully reconstructed &Lambda⁰/&Sigma^- hyperons. They do mean that we have identified the final states,

K^- + ⁴He -> &Lambda + n + d

, and

K^- + ⁴He -> &Sigma^- + p + d

. Then, it is possible to introduce hyperon 3-momentum p_Y(1:3) and Mmiss being defined by

vec(p_Y)=-(vec(p_d)+vec(p_N)),

M_miss=sqrt((M_⁴He+M_K^--E_N)²-P_N²)

, and treat them as hyperon 3-momentum and Yd invariant mass. The &Lambda/&Sigma^- are defined as

p_n.le.400 MeV/c .AND. ⁴He(stopped K^-,dn)Y⁰ mass within (1100.,1150.) MeV/c²:&Sigma^-

⁴He(stopped K^-,dp)Y^- mass within (1180.,1220.) MeV/c²:&Lambda

&Lambda d result from dn back-to-back events

&Sigma^- d result from dp back-to-back events