Today's Progress 29. May. 2007
&Lambda reconstruction/&Lambda N correlation analysis: E570
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onNT) events
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events from E570 1st cycle. The black-colored spectra are results when &Lambda decay vertex is adopted to calculate 1/&beta and energy loss inside, while the red-colored ones are the result with Kaon stopping point defined by BLC-PDC.
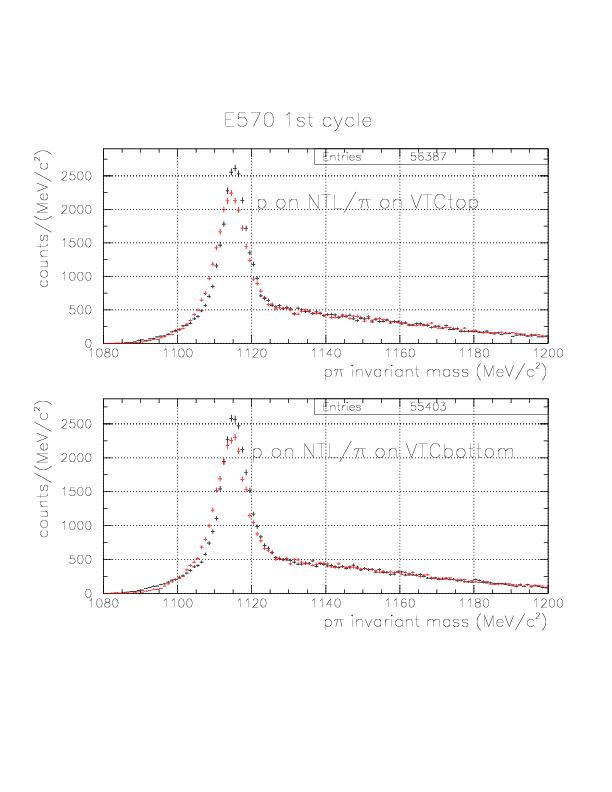
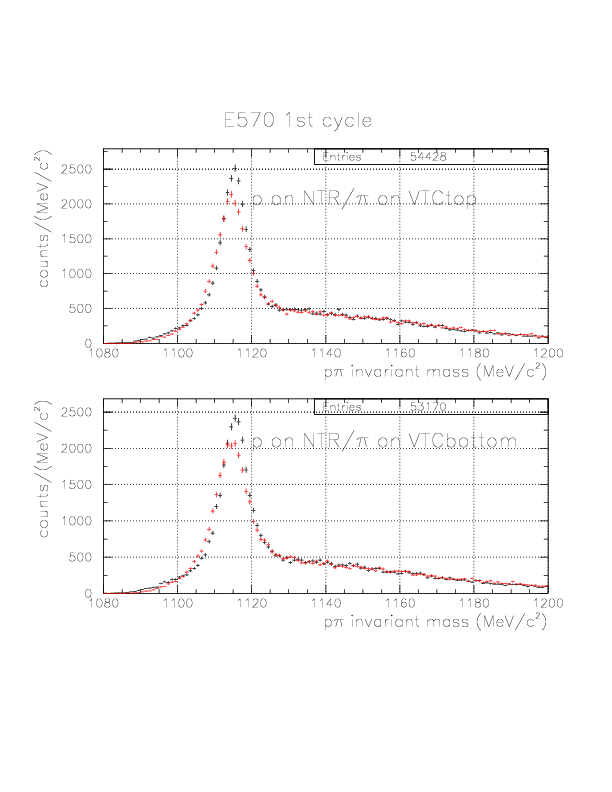
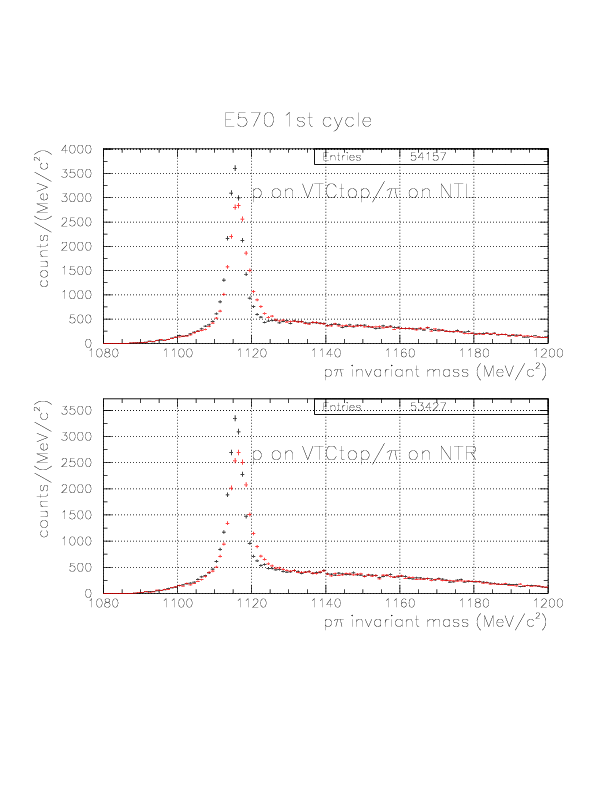
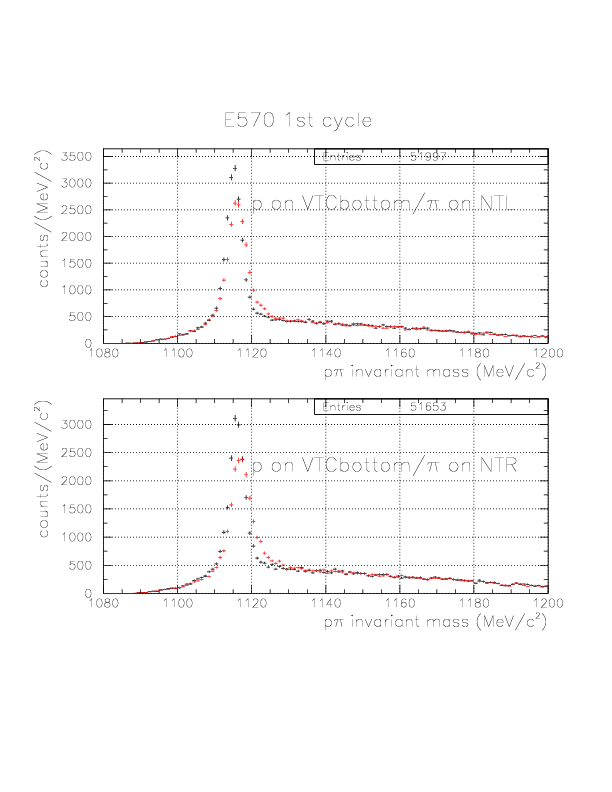
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events from E570 2nd cycle.
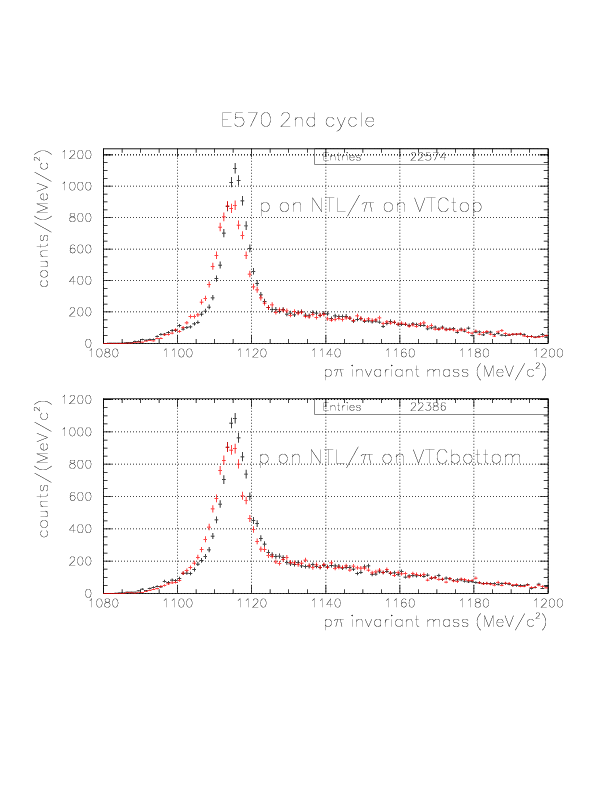
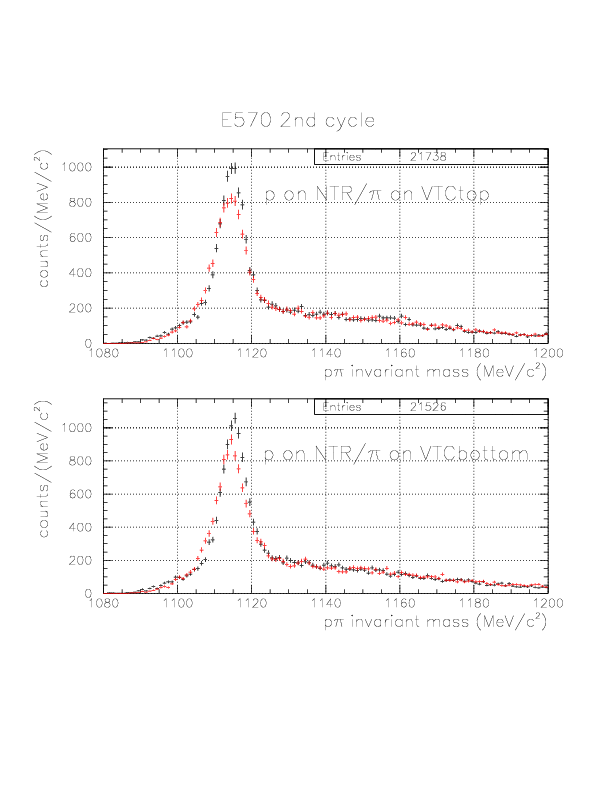
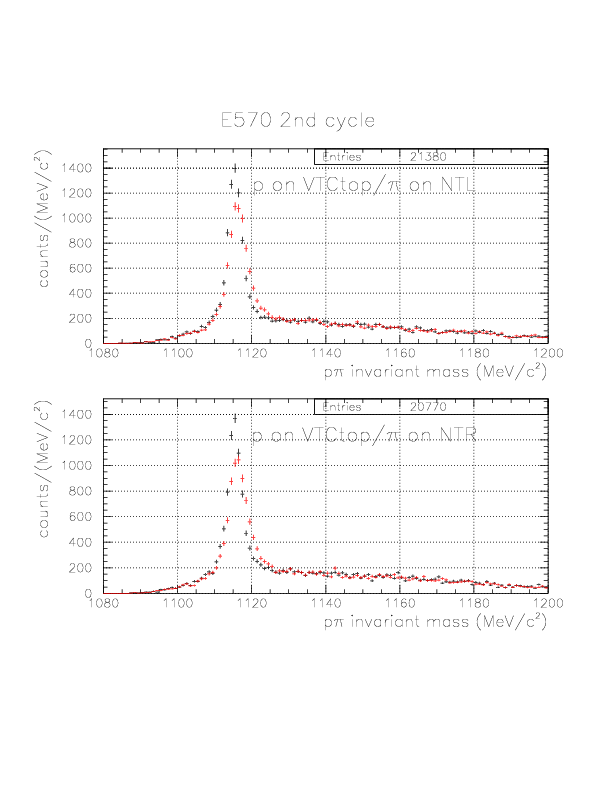
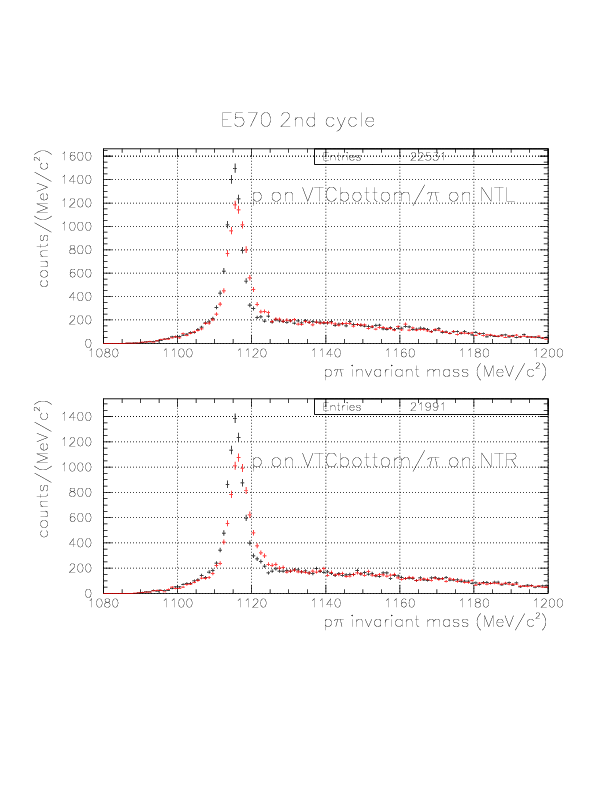
Suppression of combinatorial background by vertex information
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events for E570 1st cycle. The events with positive vec(v&Lambda)*hat(p&Lambda) are plotted by red, while green if not.
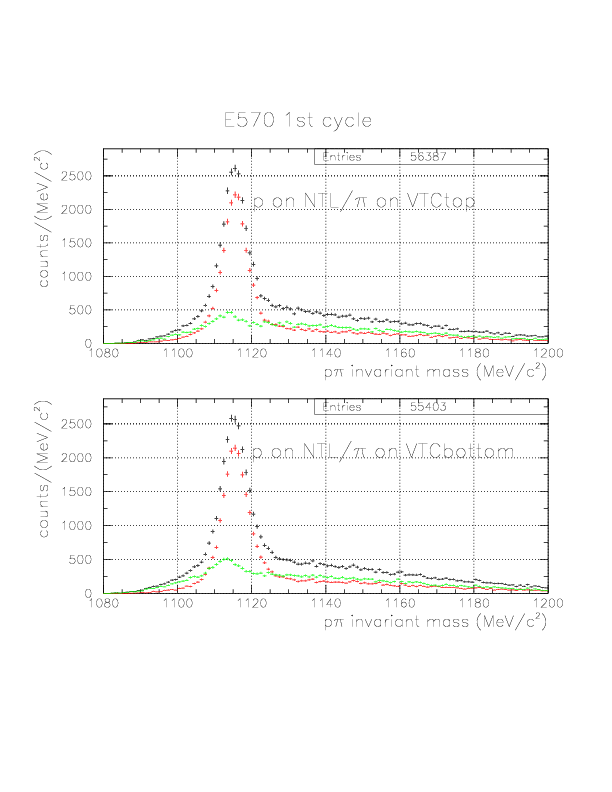
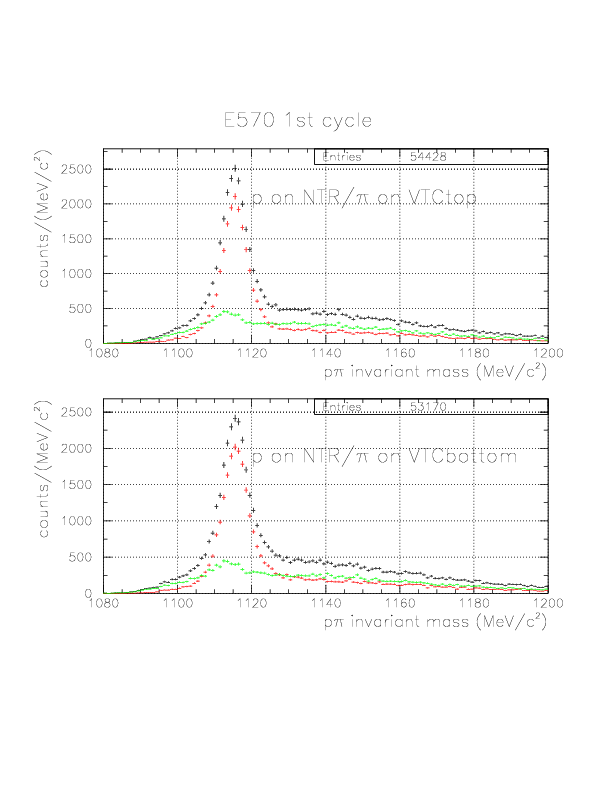
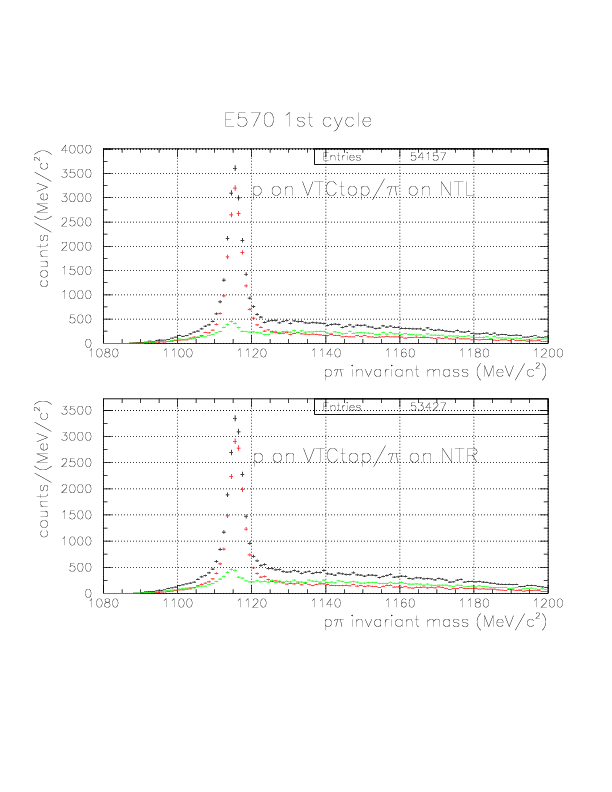
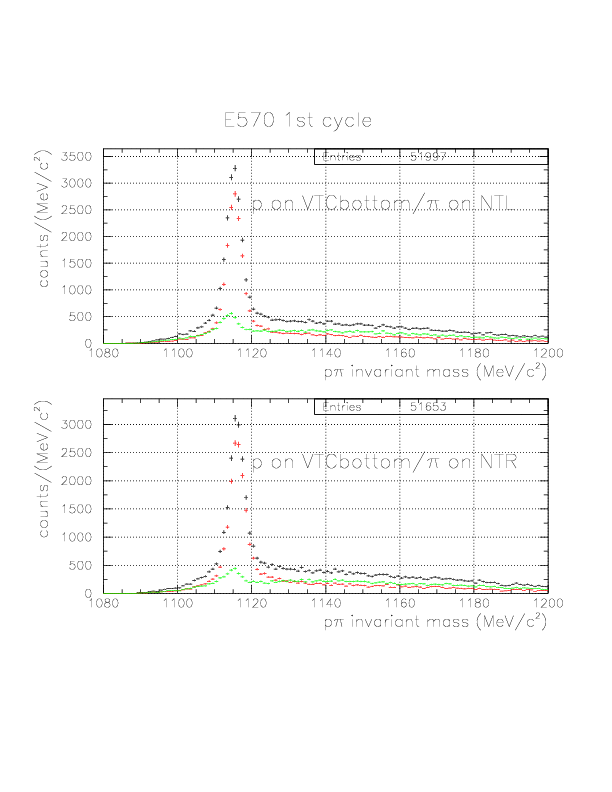
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events for E570 2nd cycle. The events with positive vec(v&Lambda)*hat(p&Lambda) are plotted by red, while green if not.
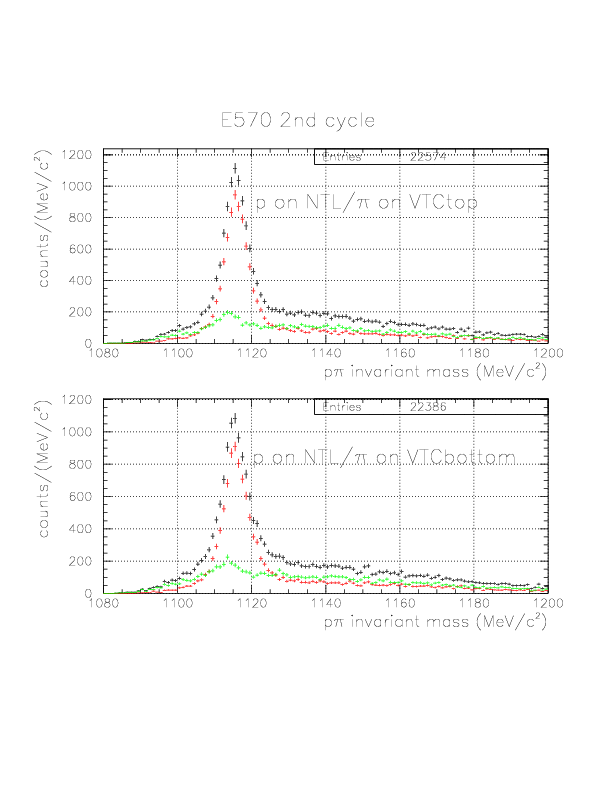
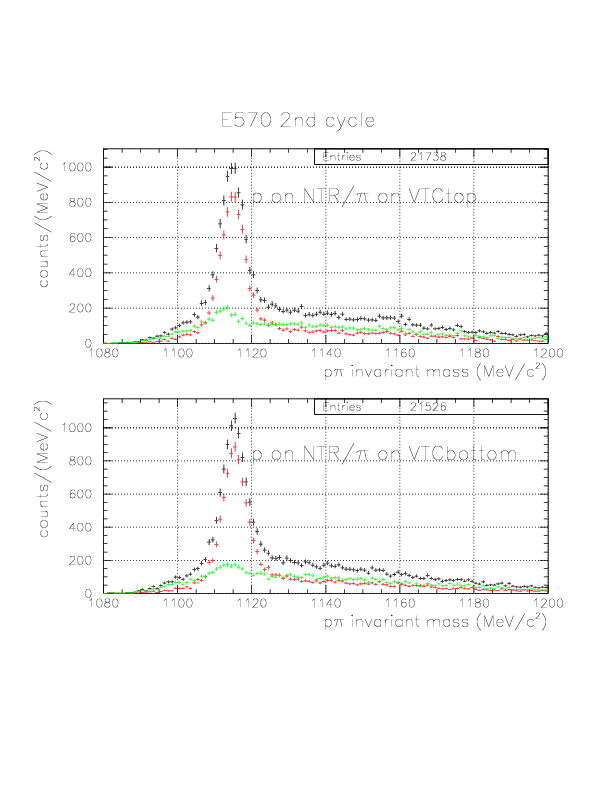
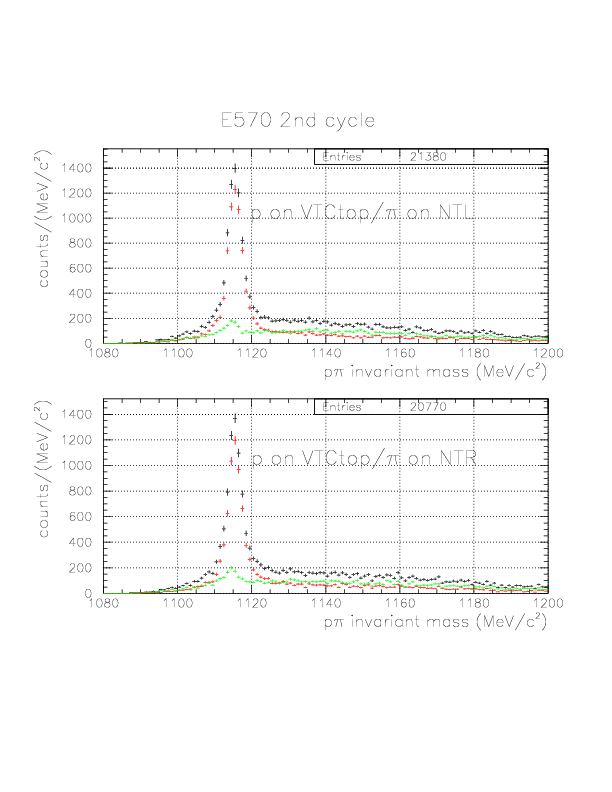
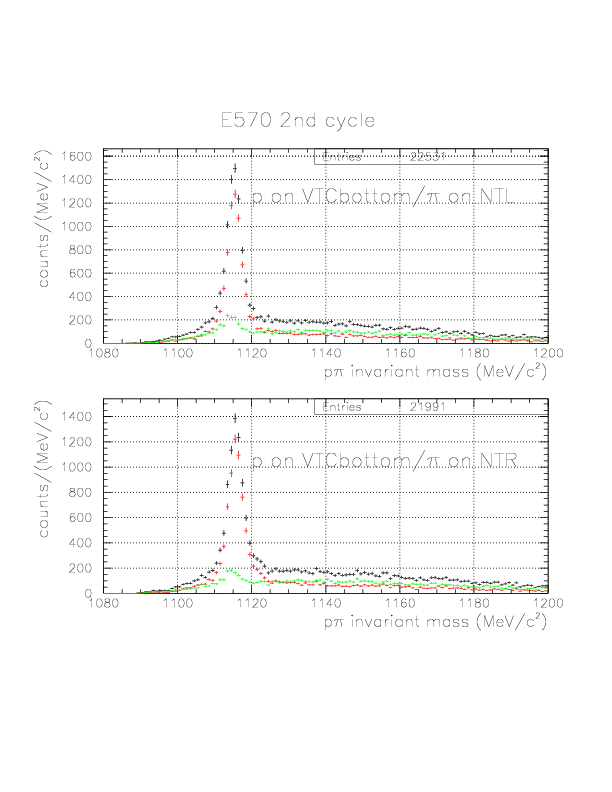
p&pi invariant mass spectra for specific event sets
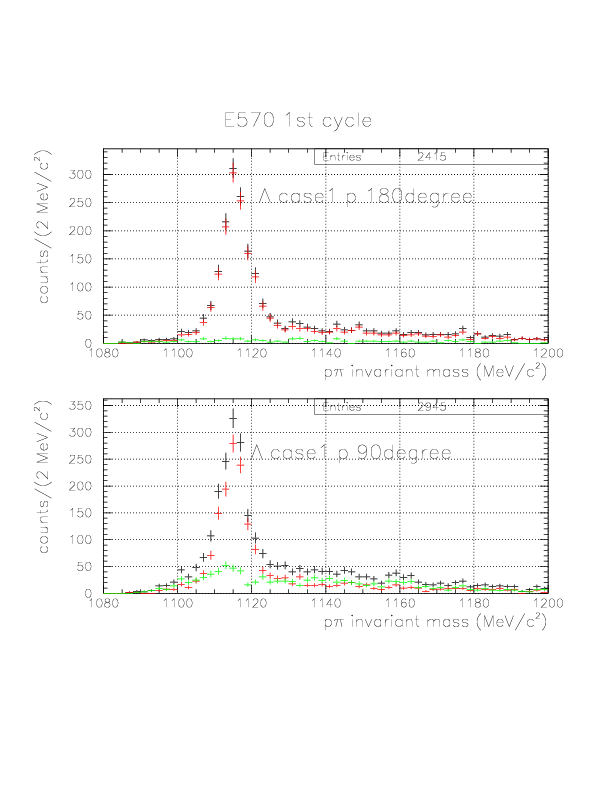
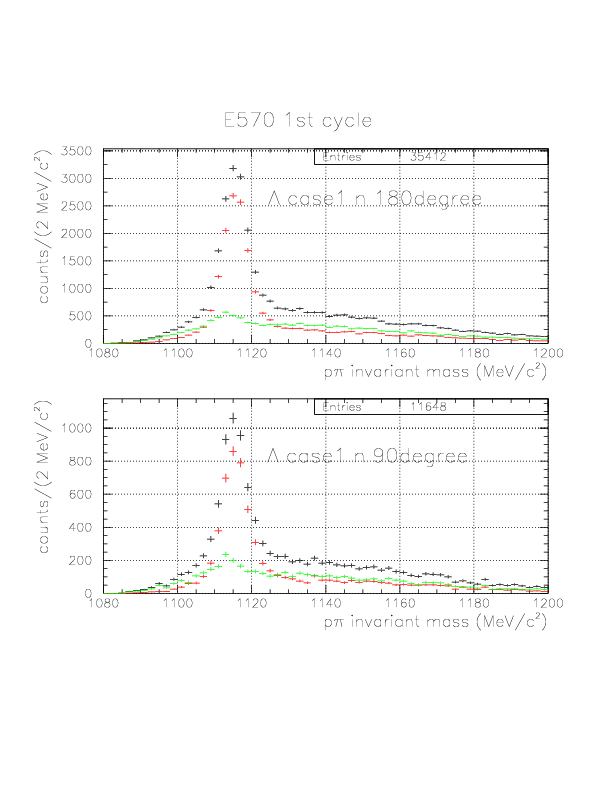
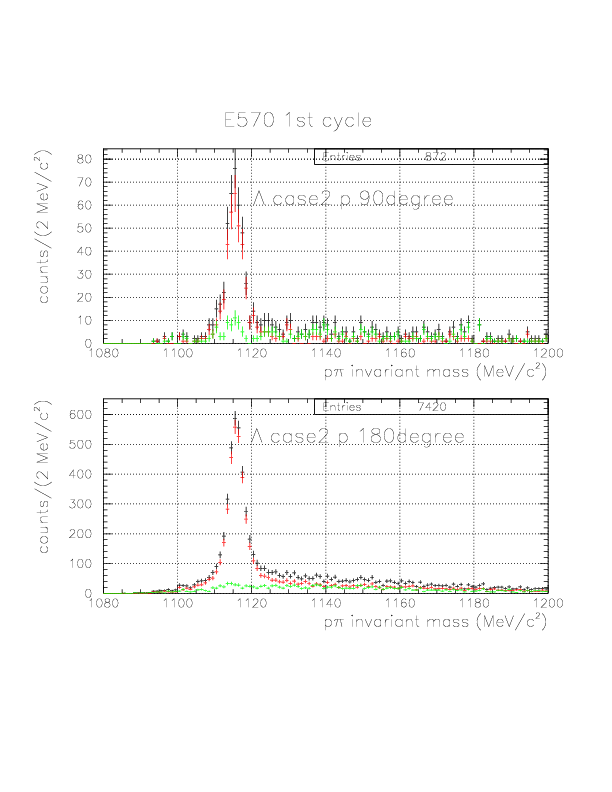
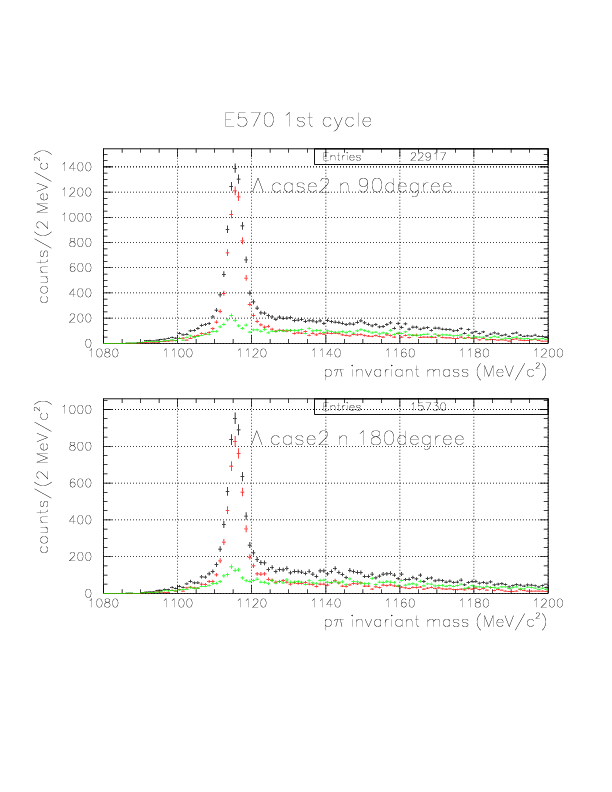
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events from E570 1st cycle. The events with positive vec(v&Lambda)*hat(p&Lambda) are plotted by red, while green if not. Event topology is explicitly written on the spectra.
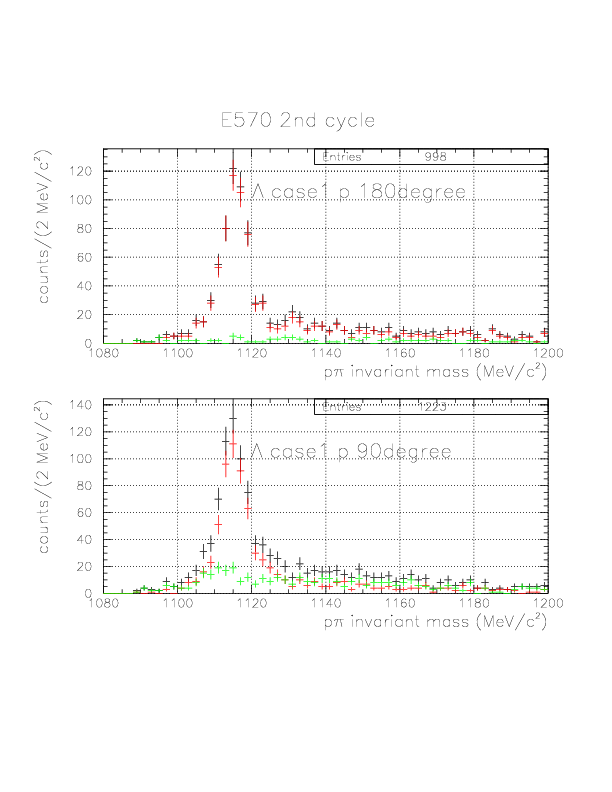
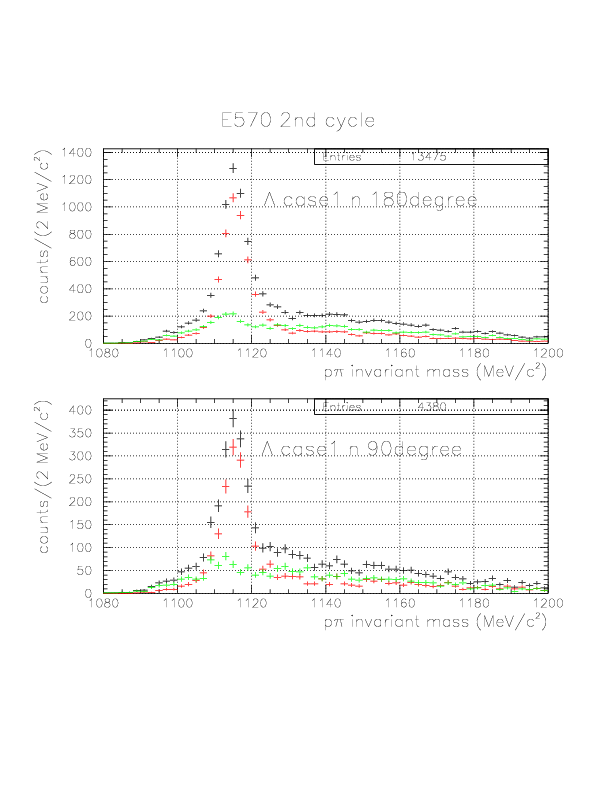
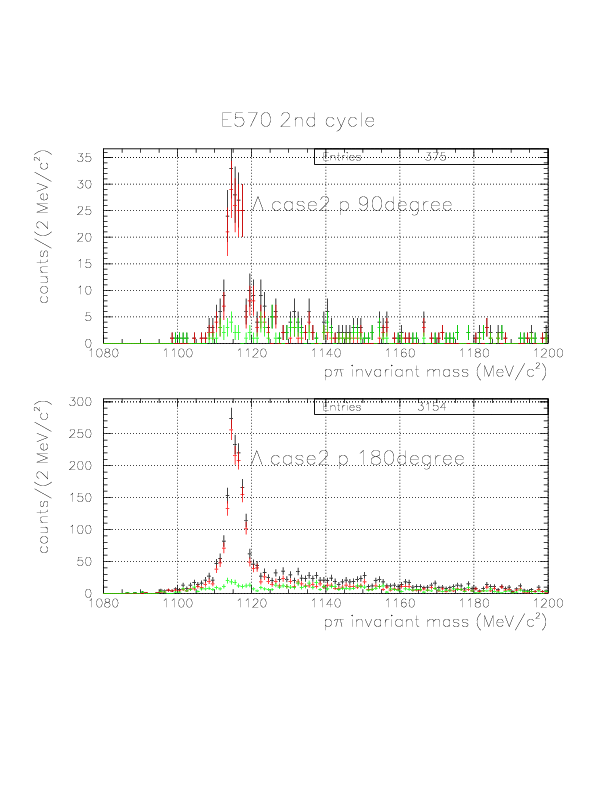
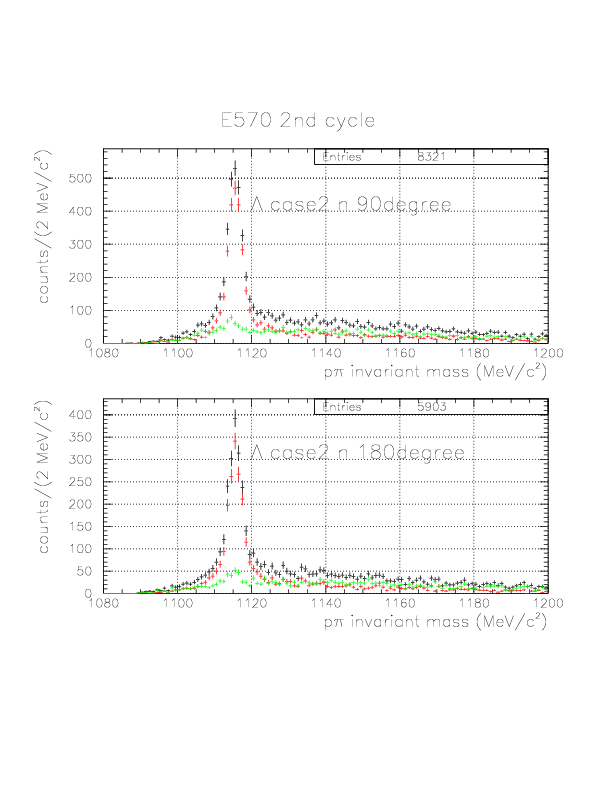
p&pi invariant mass spectra constructed from (p onNT, &pi onTC) and (p onTC, &pi onTC) events from E570 2nd cycle.
&Lambda N correlation analysis
E570 cycle-by-cycle &Lambda N event statistics. For the primary neutron, selection A is defined by detection software threshold (3 MeVee) and 1/&beta selection (1.6-9.0) to define physical ones. For the primary proton, it is defined by successfull energy loss correction with 'reaction vertex' and layer B hit if the proton is measured on TC. Selection B is defined by the elimination of unhealthy PB counter hit(nothing for 1st cycle, R-15 for 2nd cycle).
| YN pair(dibaryon/tribaryon channel) | case ID(Selection) | Angler acceptance | PA/PB/NT particle | TC particle | No. of reconstructed &Lambda | No. of event after A | No. of event after B (yield of well-defined &Lambda N pair) |
|---|
| &Lambda p (X+/S0) | 1(A-b-1-x) | 180 +- 30 | p + p | &pi | 1294/514 | 1256/494 | 1256/467 |
| &Lambda p (X+/S0) | 1(A-b-x-1') | 90 +- 45 | p | &pi + p | 1186/490 | 916/379 | 916/372 |
| &Lambda n (X0/S+) | 1(A-b-3-x) | 180 +- 30 | p + n | &pi | 12289/4678 | 4550/1875 | 4550/1841 |
| &Lambda n (X0/S+) | 1(A-b-x-3') | 90 +- 45 | p | &pi + n | 3908/1389 | 1678/614 | 1678/600 |
| &Lambda p (X+/S0) | 2(B-a-1-x) | 90 +- 45 | &pi + p | p | 337/157 | 323/149 | 323/142 |
| &Lambda p (X+/S0) | 2(B-a-x-1') | 180 +- 45 | &pi | p + p | 3002/1277 | 2476/1050 | 2476/1027 |
| &Lambda n (X0/S+) | 2(B-a-3-x) | 90 +- 45 | &pi + n | p | 6626/2434 | 1357/532 | 1357/516 |
| &Lambda n (X0/S+) | 2(B-a-x-3') | 180 +- 45 | &pi | p + n | 4438/1678 | 2489/989 | 2489/950 |
The definition of variables are as follows:
&Lambda 4-momentum p&Lambda(0:3)/3-momentum p'&Lambda(3):p'&Lambda(i)=pp(i)+p&pi(i), p&Lambda(i)=p'&Lambda(i) (i=1,2,3), p&Lambda(0)=sqrt(M&Lambda2+|p'&Lambda|2),
Nucleon 4-momentum pN(0:3)/3-momentum p'N(3):pN(i)=p'N(i) (i=1,2,3), pN(0)=sqrt(MN2+|p'N2|)
cos(N&Lambda):p'&Lambda*p'N/(|p'&Lambda|*|p'N|)
N&Lambda total 3-momentum Ptot:sqrt((p&Lambda(1)+pN(1))2+(p&Lambda(2)+pN(2))2+(p&Lambda(3)+pN(3))2)
N&Lambda total energy Etot:p&Lambda(0)+pN(0)
N&Lambda invariant mass Minv:sqrt(Etot2-Ptot2)
4He(stopped K-,N&Lambda)X missing mass Mmiss:sqrt((M4He+MK--Etot)2-Ptot2)
The results are exhibitted below for every event topologies:
&Lambda case 1 p 180degree
&Lambda case 1 p 90degree
&Lambda case 1 n 180degree
&Lambda case 1 n 90degree
&Lambda case 2 p 180degree
&Lambda case 2 p 90degree
&Lambda case 2 n 180degree
&Lambda case 2 n 90degree























