1. Re-define the reaction vertex with proton/&pi tracks. Then, proton/&pi vertex is more accurately given for &Lambda->p&pi events. This is extremely important, because the procedure 2 does not work correctly, otherwise.
2. Re-define proton/pion TOF from its generation to PA arrival by energy-loss correction, by newly-defined p&pi vertex, and perform PA-TC TOF measurement for &pi/p.
3. Estimate initial momentum of VTC-detected p/&pi by energy-loss correction procedure as for NT-detected particles, with the reaction vertex and re-calculated TOF.
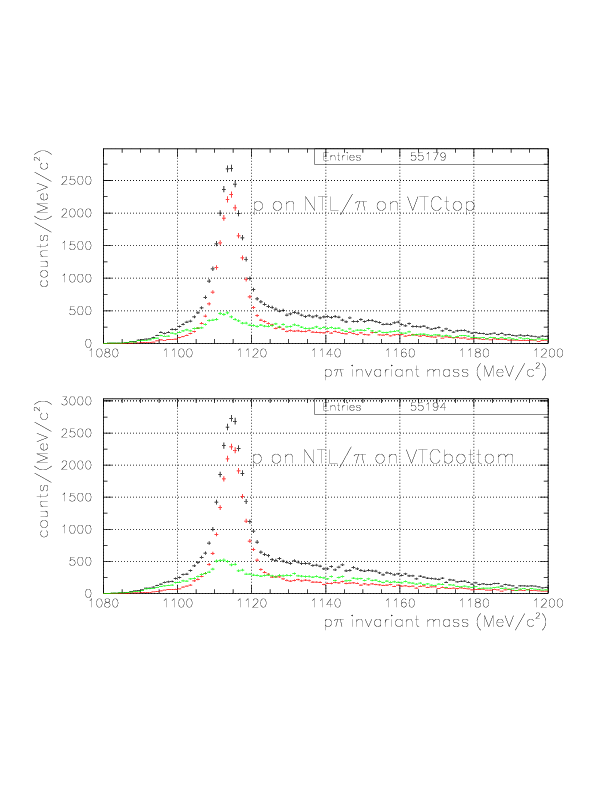
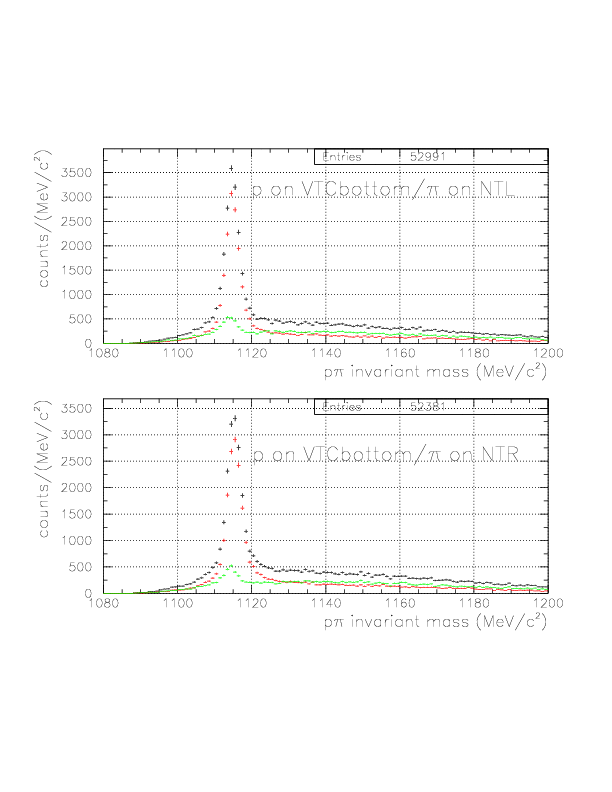
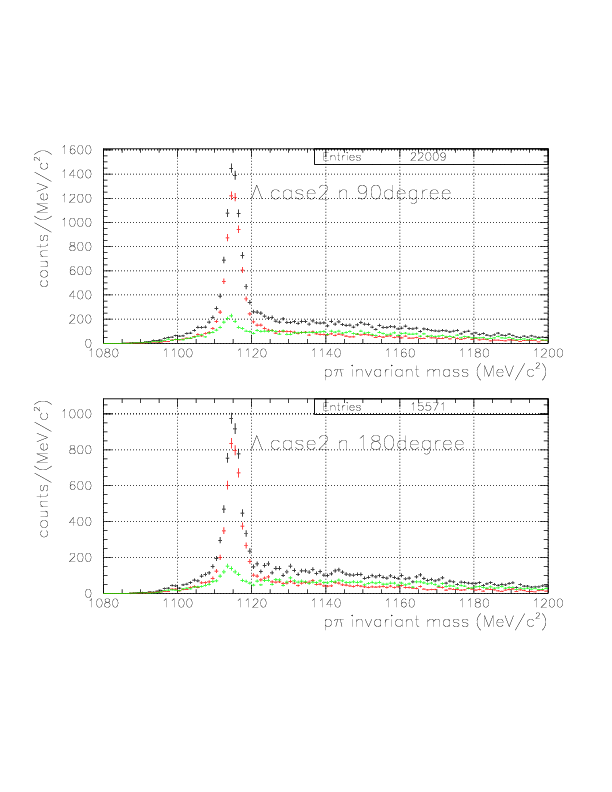
By the newly-defined decay vertex and PA-TC TOF analysis, we expect better accuracy of the p/&pi momentum for both of TC/NT sides, hence improved p&pi invariant mass. The comparisons are shown below for various event patterns. The red is constructed with old(BLC-PDC) vertex and T0->TC TOF analysis, while the black is the improved ones.
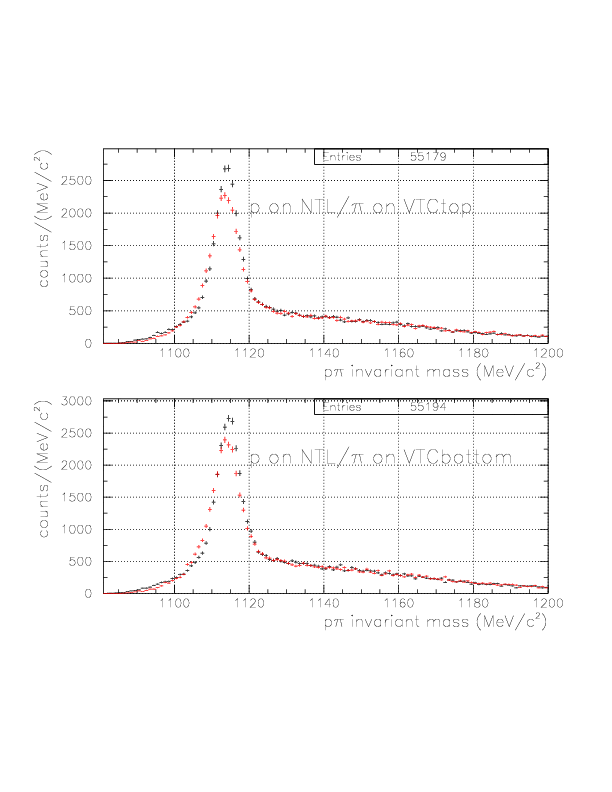
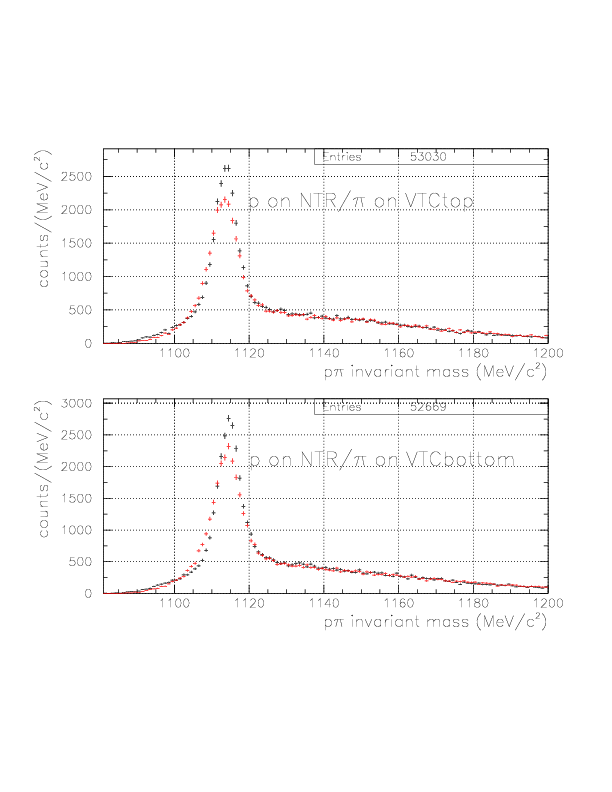
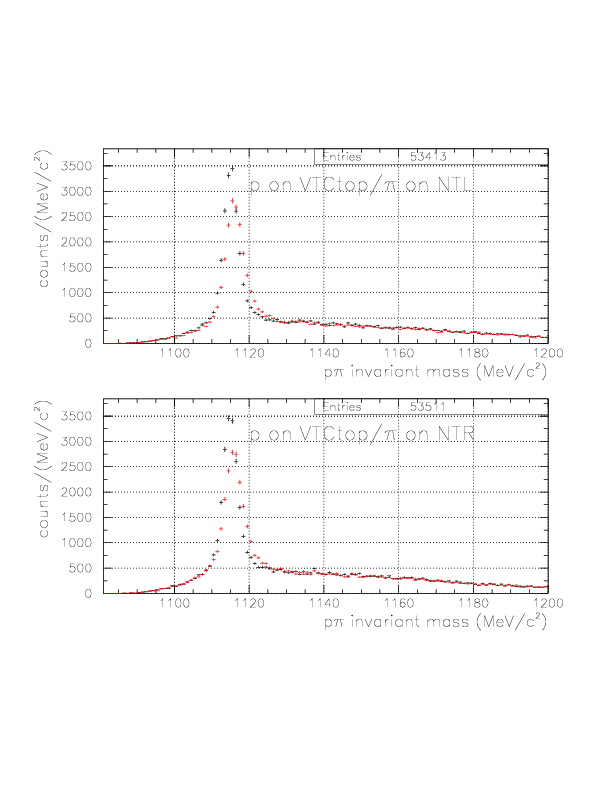
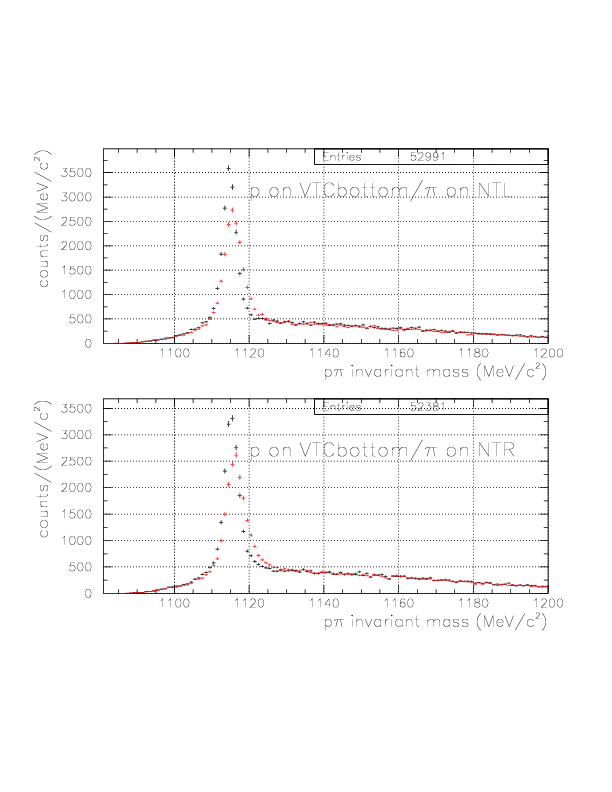
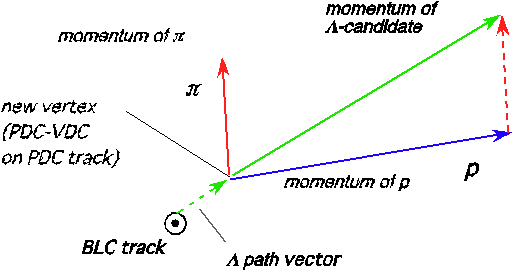
In order to suppress the combinatorial BG in general case, we introduce &Lambda path vector, which is defined by the vector defined by BLC-track and new vertex, and momentum of &Lambda candidates. The definition is as follows:
1. new vertex and 3-momentum of the &Lambda candidate defines a straight line (A) in the E549 global coordinate.
2. The closest approaching points between BLC track and the straight-line is defined.
3. The vector connects the point on the straight line A and new vertex are defined as &Lambda path vector
When the &Lambda path vector vec(v&Lambda) is defined as described, then the inner product vec(v&Lambda)*hat(p&Lambda) is expected to work for S/N improvement. Here, hat(p&Lambda) is an unit vector with the direction of &Lamda candidate momentum.
 The results are shown below.
The results are shown below.
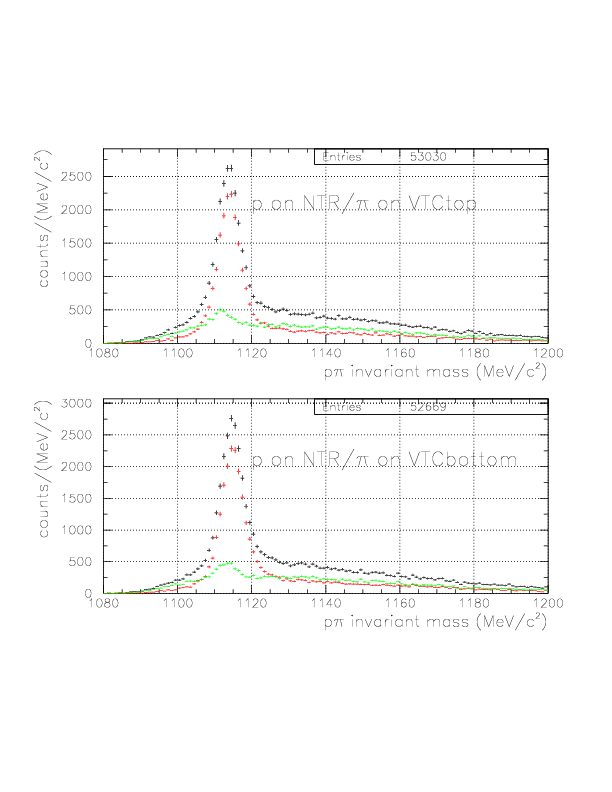
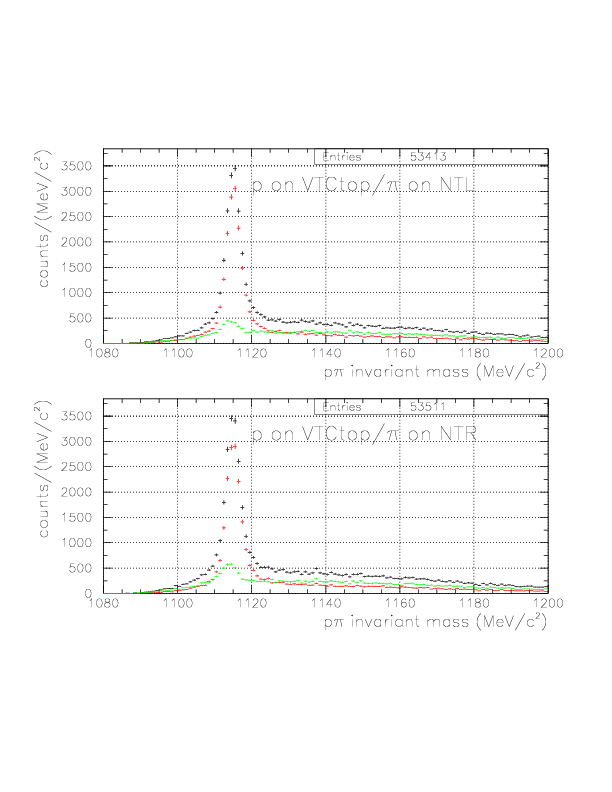
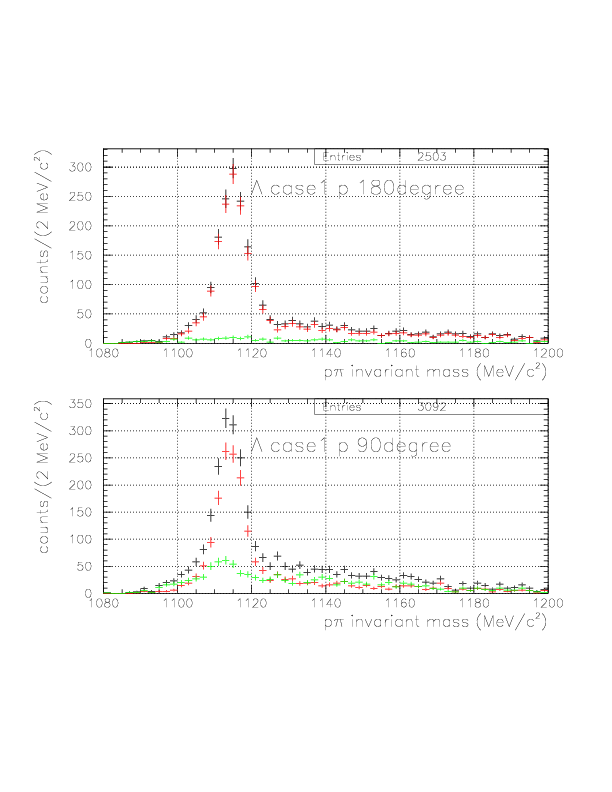
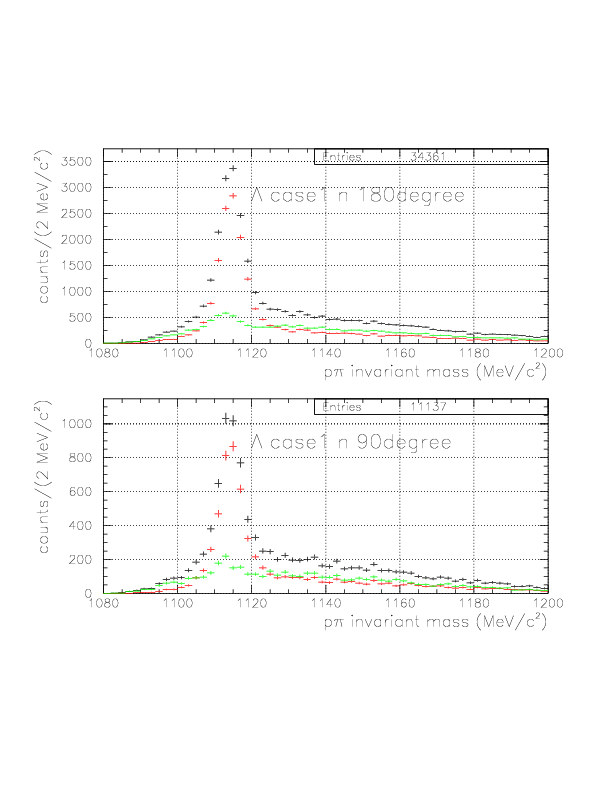
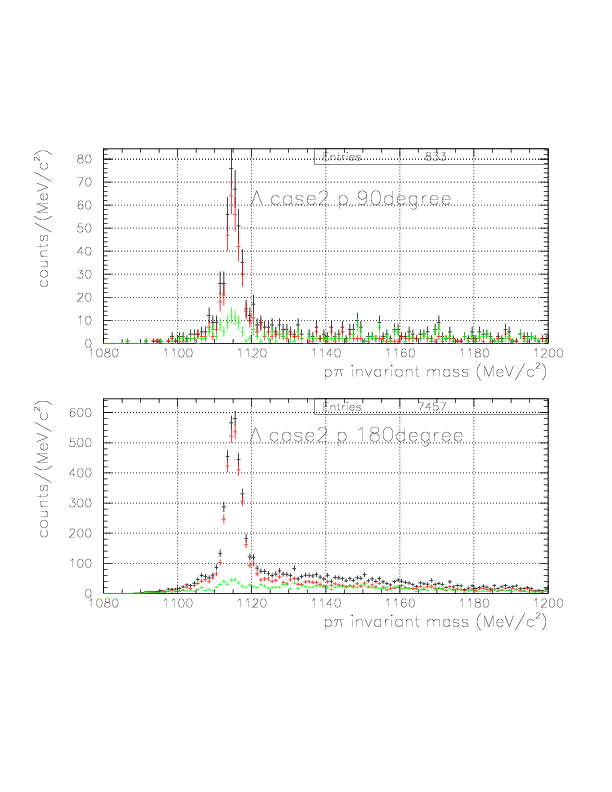
1. vec(v&Lambda)*hat(p&Lambda) is positive.
2. p&pi invariant mass value is within (1108.,1124.), (1111.,1121.) for case1 and case2, respectively.
The first requiremnt is imposed to improve S/N ratio, by factor ~2 with ~90% signal survival rate.
| YN pair(dibaryon/tribaryon channel) | case ID(Selection) | Angler acceptance | PA/PB/NT particle | TC particle | No. of reconstructed &Lambda | No. of event after A | No. of event after B (yield of well-defined &Lambda N pair) |
|---|---|---|---|---|---|---|---|
| &Lambda p (X+/S0) | 1(A-b-1-x) | 180 +- 30 | p + p | &pi | 1329 | 1271 | 1164 |
| &Lambda p (X+/S0) | 1(A-b-x-1') | 90 +- 45 | p | &pi + p | 1217 | 937 | 884 |
| &Lambda n (X0/S+) | 1(A-b-3-x) | 180 +- 30 | p + n | &pi | 12200 | 4555 | 4353 |
| &Lambda n (X0/S+) | 1(A-b-x-3') | 90 +- 45 | p | &pi + n | 3711 | 1675 | 1593 |
| &Lambda p (X+/S0) | 2(B-a-1-x) | 90 +- 45 | &pi + p | p | 313 | 297 | 268 |
| &Lambda p (X+/S0) | 2(B-a-x-1') | 180 +- 45 | &pi | p + p | 2901 | 2416 | 2310 |
| &Lambda n (X0/S+) | 2(B-a-3-x) | 90 +- 45 | &pi + n | p | 6406 | 1383 | 1309 |
| &Lambda n (X0/S+) | 2(B-a-x-3') | 180 +- 45 | &pi | p + n | 4376 | 2460 | 2357 |
The definition of variables are as follows:
&Lambda 4-momentum p&Lambda(0:3)/3-momentum p'&Lambda(3):p'&Lambda(i)=pp(i)+p&pi(i), p&Lambda(i)=p'&Lambda(i) (i=1,2,3), p&Lambda(0)=sqrt(M&Lambda2+|p'&Lambda|2),
Nucleon 4-momentum pN(0:3)/3-momentum p'N(3):pN(i)=p'N(i) (i=1,2,3), pN(0)=sqrt(MN2+|p'N2|)cos(N&Lambda):p'&Lambda*p'N/(|p'&Lambda|*|p'N|)
N&Lambda total 3-momentum Ptot:sqrt((p&Lambda(1)+pN(1))2+(p&Lambda(2)+pN(2))2+(p&Lambda(3)+pN(3))2)
N&Lambda total energy Etot:p&Lambda(0)+pN(0)
N&Lambda invariant mass Minv:sqrt(Etot2-Ptot2)
4He(stopped K-,N&Lambda)X missing mass Mmiss:sqrt((M4He+MK--Etot)2-Ptot2)
The results are exhibitted below for every event topologies: