Today's Progress 2. Feb. 2007

A better identification procedure of &Lambda

Until now, we had some ambiguities on &pi detection on TC, as listed below:

The &pi flight distance. Now, the &pi generation point is given by the closest approach of BLC and PDC tracks + Vca vector.

The &Lambda life time. The measured TOF is now including the &Lambda life time, hence a &pi momentum looks more smaller than the realistic value.

Ionization energy loss of &pi^- from the generation up to the detection.

Since we have proton/&pi tracks separately, we can improve the &Lambda identification as follows.

Method

1. Re-define the reaction vertex with proton/&pi tracks. Then, proton/&pi vertex is more accurately given for &Lambda->p&pi events. This is extremely important, because the procedure 2 does not work correctly, otherwise.

2. Re-define proton TOF from its generation to PA arrival by energy-loss correction, by newly-defined p&pi vertex, and perform PA-TC TOF measurement for &pi. Or, calculate TOF distance of &Lambda and get TOF(&Lambda) directly assuming p&pi pair is from &Lambda decay (Then, &Lambda momentum and decay vertex are known, hence TOF distance can be calculated as the distance between decay vertex and reaction vertex which can be defined as the closest approaching point of kaon track and a strainght line defined by &Lambda momentum and decay vertex). The two alternative ways are illustrated below.

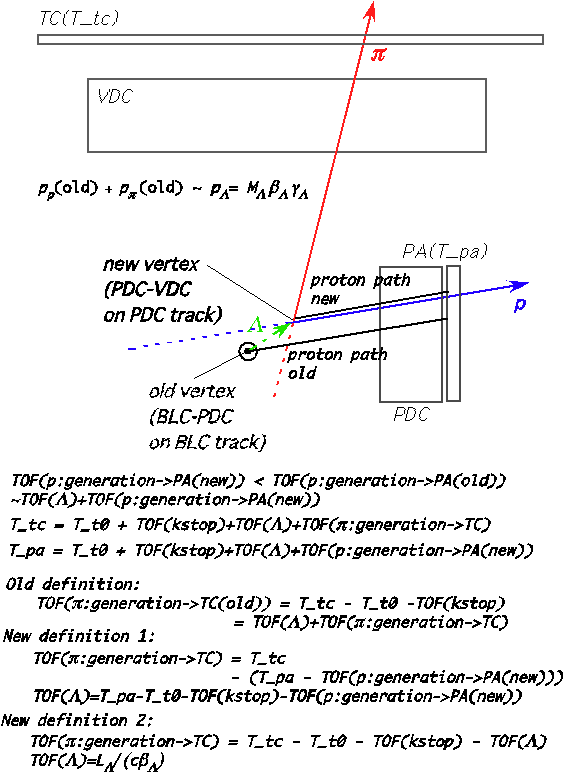
3. Estimate initial momentum of &pi by energy-loss correction procedure as for proton, with the reaction vertex and re-calculated TOF.

Then, we expect some improvements on the &Lambda central mass and width on the p&pi invariant mass spectra. Note that this analysis properly works ONLY IF p&pi pair is from &Lambda decay, and if the p/&pi pair is NOT from &Lambda decay, it introduces certain systematics on the p/&pi momentum. Therefore, we adopt this analysis ONLY for n&Lambda/p&Lambda invariant mass construction.

Results

Comparison of two vertices for &Lambda->p&pi^- from p&Lambda events

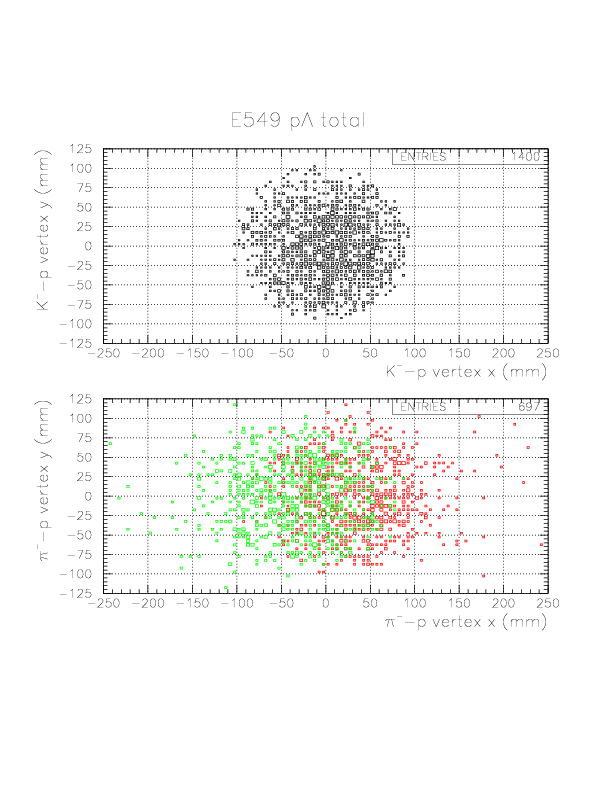
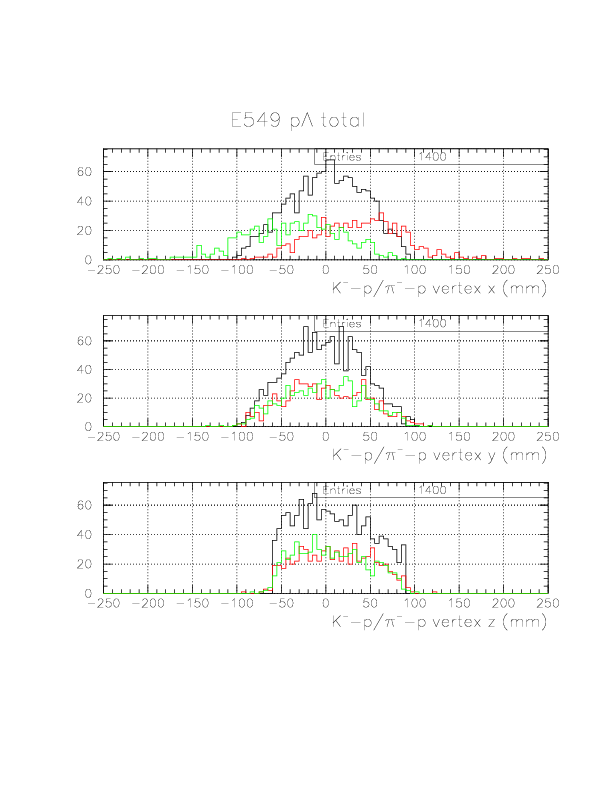
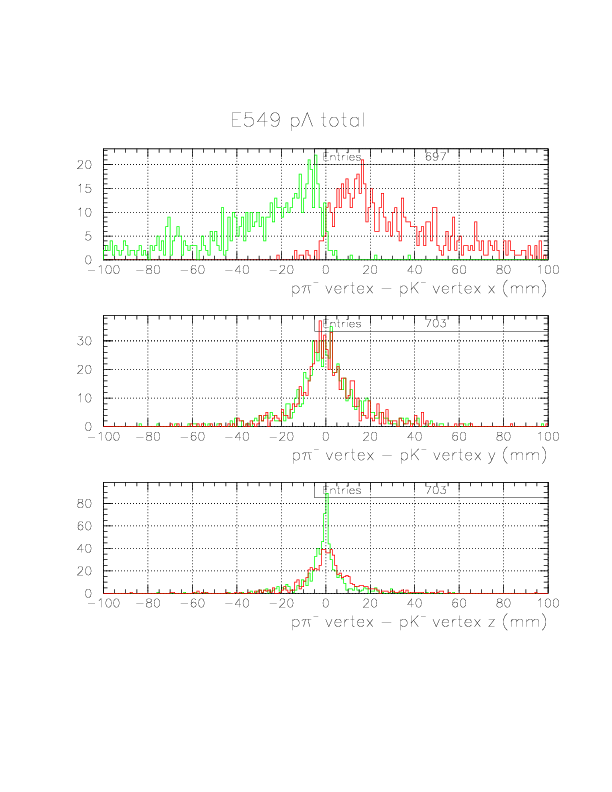
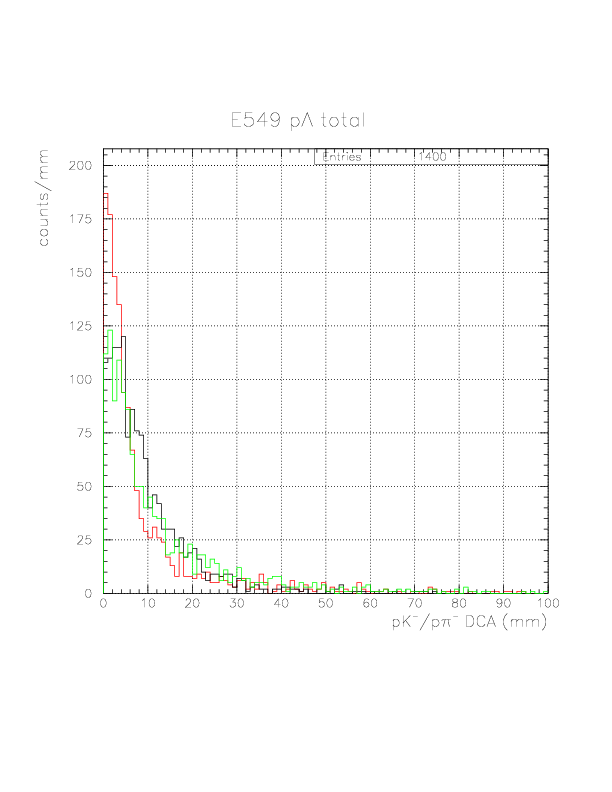
As shown below for p&Lambda events, x-motion of &Lambda is very clearly seen in the comparison of K^^--p(Rarm)/&pi^--p(&Lambda decay) vertices. For n&Lambda events, K^-p/&pi^-p pair is unique, hence we do not need to care about that issue.

(1st,2nd)Comparison of two different reaction vertices from p&Lambda events. Black color is used for K^- - p vertex, to which the proton is detected by the Rarm. The red is the case if the decay proton is detected by the Larm, while the green is by the Rarm. (3rd)Difference of two vertices, defined as p&pi vertex position - K^-p vertex position. The red/green are used to represent L/R arms, respectively. The &Lambda motion to x-direction is clearly seen. (4th) Comparison of the DCA from p&Lambda events. The green is K^--p DCA, to which the proton comes from Rarm. The red is &pi^--p DCA, to which the p&pi pair comes from &Lambda decay. The green is &pi^--p DCA, to which the proton comes from primary reaction, and &pi comes from &Lambda decay.

Lifetime of &Lambda and p&pi invariant mass spectrum by procedure (1)

If we re-calculate TOF(p:generation->PA |new) by newly-defined decay vertex, we may be able to observe event-by-event &Lambda lifetime(=TOF), by

TOF(&Lambda) = T_pa - T_t0 - TOFkstop(z) - TOF(p:generation->PA | new).

Then,

TOF(&pi:generation->TC) = T_tc - T_t0 - TOFkstop(z) - TOF(&Lambda)

= T_tc - (T_pa - TOF(p:generation->PA | new))

Therefore, we re-try energy loss correction for pp/pn + &pi on TC events (only for decay proton in pp case, while proton is unique for pn case), and investigate it. It should be noted that the procedure also affect corrected proton momentum, and over-corrected momentum of protons from &Lambda decay tends to shift smaller. On this method, we re-calculate the proton momentum 3-vector by new vertex.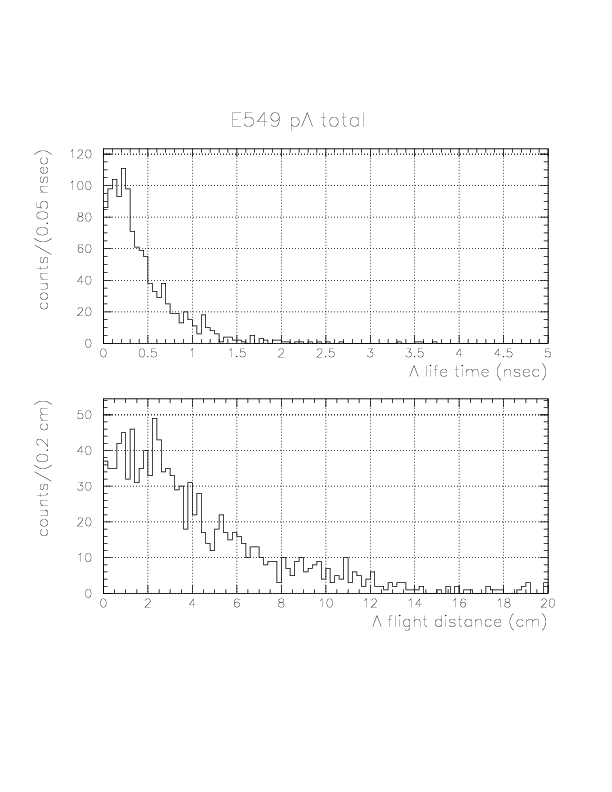

(Top) life time/flight distance spectra of &Lambda. Flight distance is calculated from &Lambda momentum and life time. (Bottom)p&pi invariant mass spectrum before(black) and after(red/green) &pi-momentum re-calculation. The red is the result with re-calculated TOF-distance of &pi, and the green is the one without it. The peak center shifts by 2 MeV/c², and re-calculated TOF distance gives better &Lambda identification.

Lifetime of &Lambda and p&pi invariant mass spectrum by procedure (2)

Alternatively, we can calculate TOF(&Lambda) directly, as

TOF(&Lambda) = L_&Lambda /(c * &beta_&Lambda).

Here, L_&Lambda is directly calculated from momentum 3-vector of &Lambda, and &beta_&Lambda is also calculated from the vector sum of pion/proton 3-momenta. By using TOF(&Lambda) in the definition, &pi TOF is re-calculated by

TOF(&pi:generation->TC) = T_tc - T_t0 - TOFkstop(z) - TOF(&Lambda),

and &pi momentum is defined again. The distribution of TOF(&Lambda), and updated p&pi invariant mass spectrum are shown below. On this method, we re-calculate the proton momentum 3-vector also by new vertex.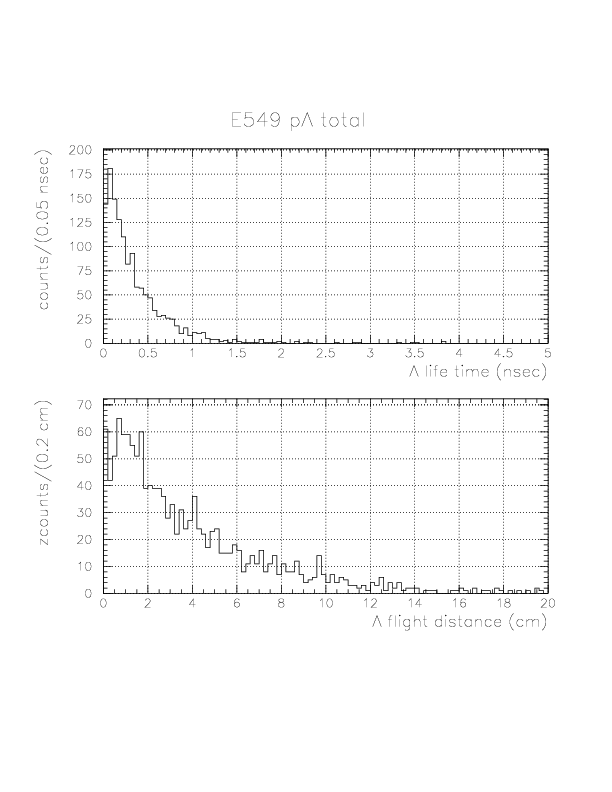

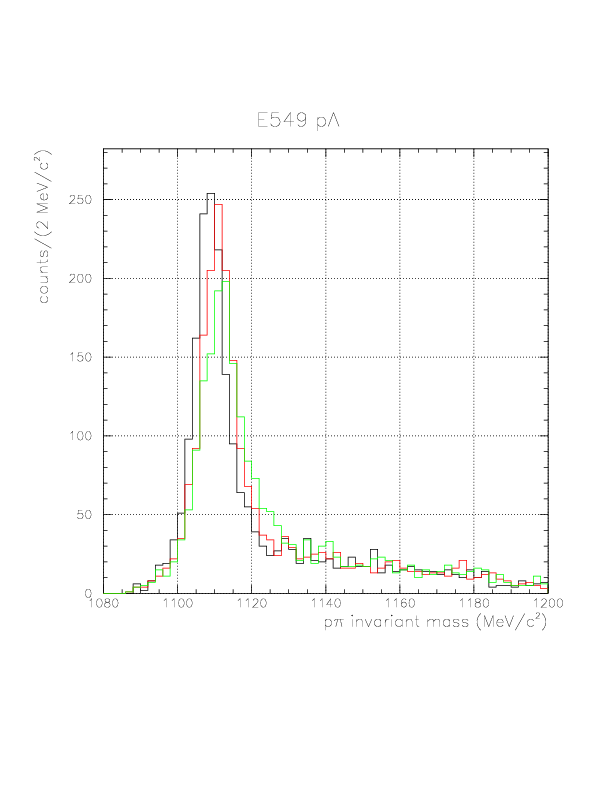
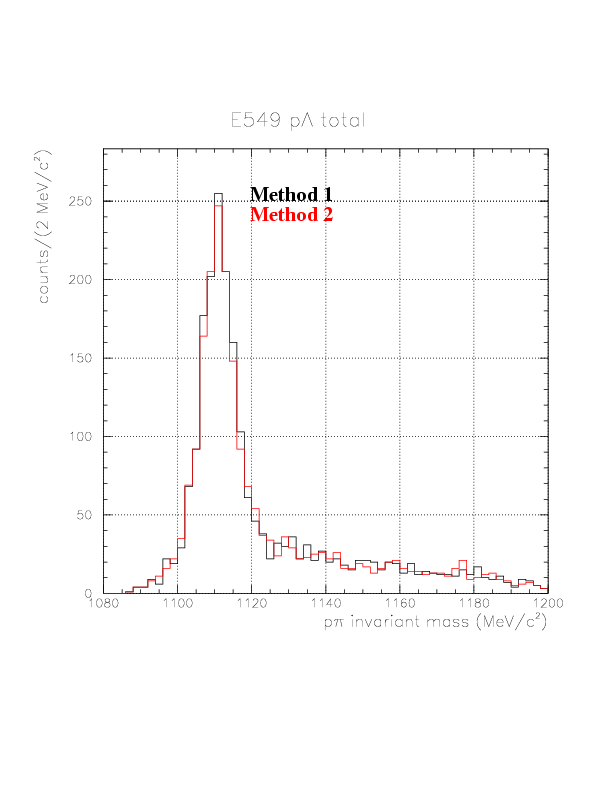
(Top) the flight distance / life time spectra of &Lambda. (Bottom) p&pi invariant mass spectra before(black) and after(red/green) &pi-momentum re-calculation. The red is the result with re-calculated TOF-distance of &pi, and the green is the one without it. The peak center shifts by 2 MeV/c², and re-calculated TOF distance gives better &Lambda identification again.

The best results from method 1/2 are now directly compared. The result from method 1 looks slightly better and we adopt it.

A comparison of p&pi invariant mass spectra obtained by 2 methods.

Ionization energy loss correction for &pi^- and finalization of p&pi invariant mass spectrum for pp + &pi on TC events

Apodpting this decay vertex definition and re-calculated TOF(&pi) by method 1, energy loss correction is performed for &pi as for proton. In order to apply energy loss correction on &pi, we impose the following requirements for 2377 pp+&pi on TC events:

1. Primary proton and decay proton energy corrections are successfully done simultaneously. 2224 out of 2377 events survive the selection.

2. pion 1/&beta is larger than 1.0 AFTER the &Lambda life-time correction. 2178 out of 2224 survive the selection.

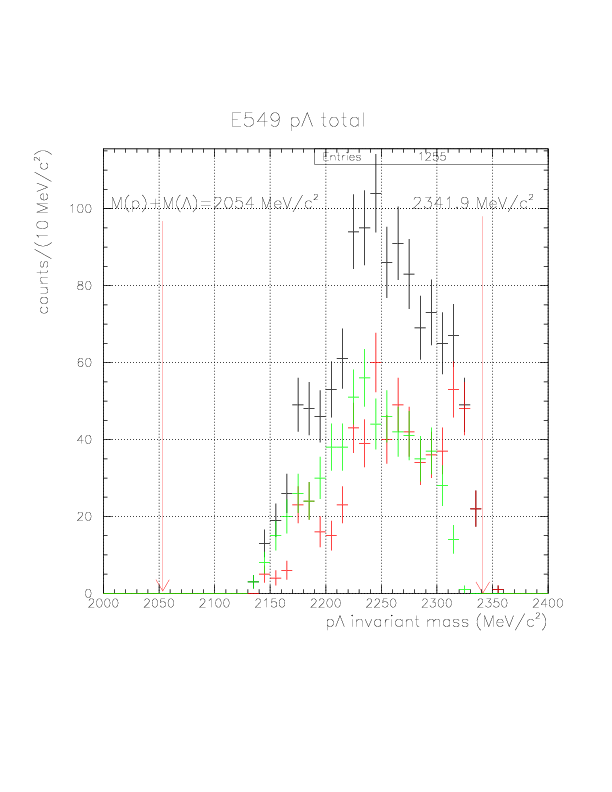
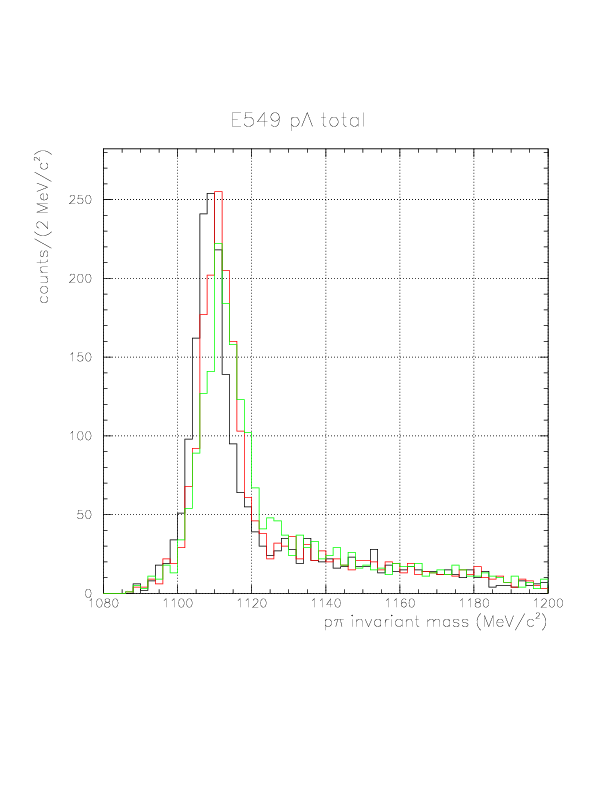
We apply the &pi energy correction for the 2178 events. The energy loss correction has not been successfully done for 48 events, because of the TC-VDC inconsistency (4 events: the pion cannot fire TC if it just goes ahead according to the detected VDC track) and vertex-TOF inconsistency (44 events:no consistent initial momentum exist). Therefore, we have obtained 2130 pp+&pi on TC events, to which corrections for p/&pi energy loss/&Lambda life time had been successfully done. The resulting p&pi invariant mass spectrum is shown below. The peak center is shifted around 1115 MeV/c², and we obtained 1217 p&Lambda events in which about (~20counts/bin*8bins=)~160 conbinatorial background from &Lambda identification is included, identifying &Lambda when p&pi invariant mass value within (1108.0,1124.0).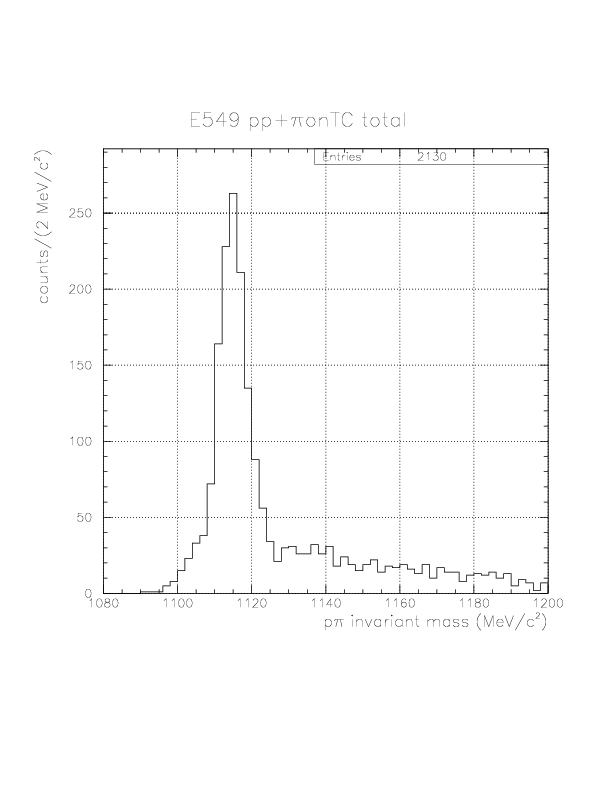

p&pi invariant mass spectrum from pp+&pi onTC events.

Ionization energy loss correction for &pi^- and finalization of p&pi invariant mass spectrum for pn + &pi on TC events

The re-definition of reaction vertex, and re-calculation of &pi and p energies at the generation are performed for pn + &pi on TC events as well. In order to apply energy loss correction on &pi, we impose the following requirements for 13488 pn+&pi on TC events:

1. Decay proton energy correction is successfully done, hence &Lambda life time is well-defined. 13058 out of 13488 events survive the selection.

2. pion 1/&beta is larger than 1.0 AFTER the &Lambda life-time correction. 12820 out of 13058 events survive the selection.

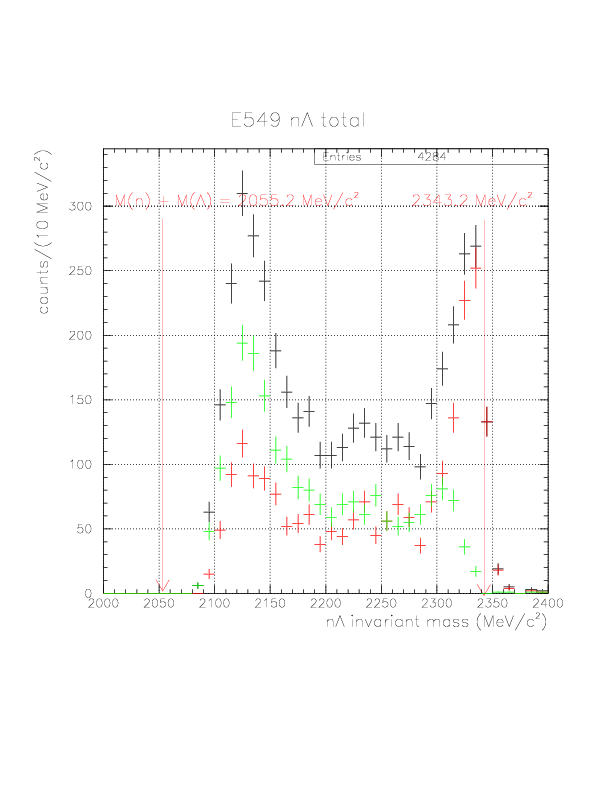
We apply the &pi energy correction for the 12820 events. The energy loss correction has not been successfully done for 407 events, because of the TC-VDC inconsistency (65 events: the pion cannot fire TC if it just goes ahead along with the detected VDC track), vertex-TOF inconsistency (342 events:no consistent initial momentum exist) and . Therefore, we have obtained 12413 pn+&pi on TC events, to which corrections for p/&pi energy loss/&Lambda life time had been successfully done. The resulting p&pi invariant mass spectrum is shown below. The peak center is shifted around 1115 MeV/c², and we obtained 4284 n&Lambda events in which about (100 counts/bin*8bins=)800 conbinatorial background from &Lambda identification is included, identifying &Lambda when p&pi invariant mass value within (1108.0,1124.0).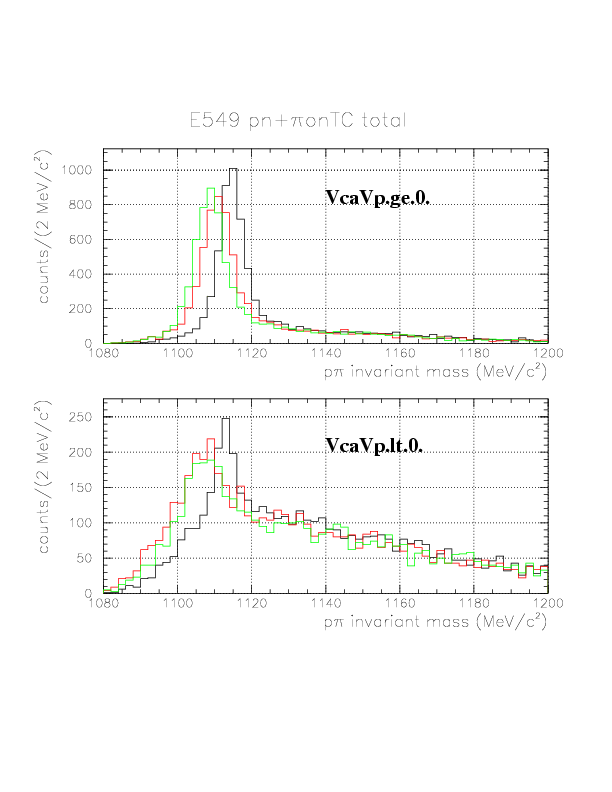

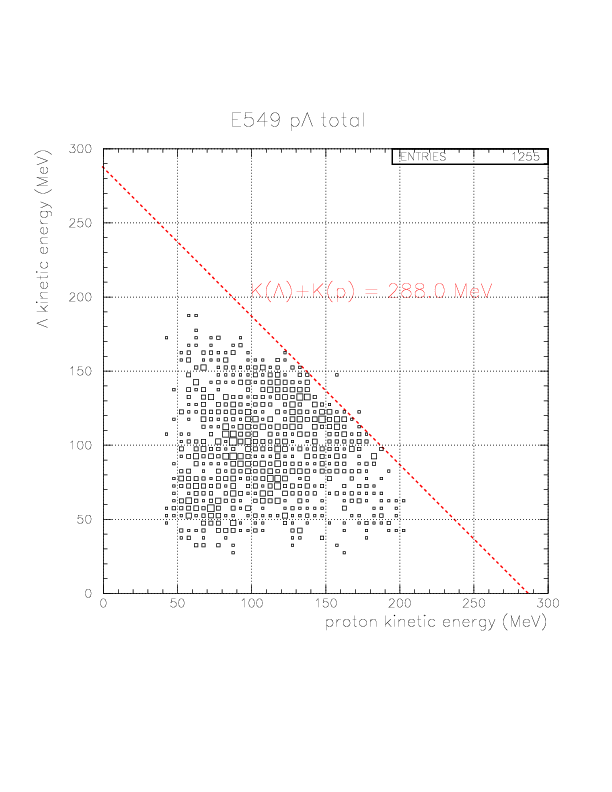
p&pi invariant mass spectra from pn+&pi onTC events. The black is the final one, while the black is the one without &Lambda lifetime/&pi energy loss corrections. The red is an intermediate one with before &pi energy loss correction but after &Lambda lifetime correction, for a comparison.

Final form of acceptance-uncorrected p&Lambda/n&Lambda invariant mass spectra

Since we have now eliminated the momentum uncertainty of &Lambda, we present the p&Lambda/n&Lambda invariant mass spectra again. Now we consider kinematical limits on the p&Lambda / n&Lambda invariant mass. Now, E(X), M(X) denote the total energy and mass of particle X, and B.E.(Y) denotes the binding energy of a nucleus Y.

p&Lambda side

M(K^-) + M(p) + M(p) -B.E.(⁴He) = E(&Lambda) + E(p)

M(K^-) + M(p) - M(&Lambda) -B.E.(⁴He) = K(&Lambda) + K(p)

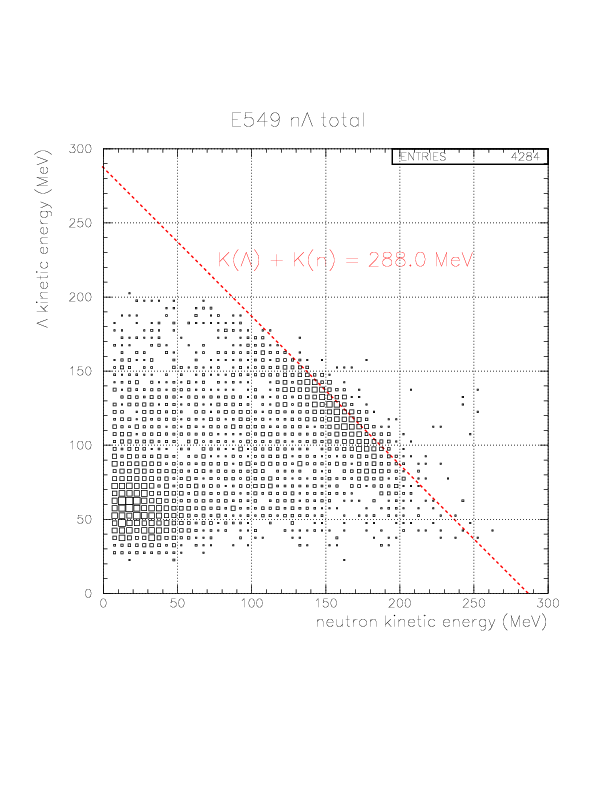
n&Lambda side:

M(K^-) + M(p) + M(n) - B.E.(⁴He) + M(p) + M(n) = E(&Lambda) + E(n) + M(p) + M(n)

M(K^-) + M(p) + M(n) - B.E.(⁴He) + M(p) + M(n) = E(&Lambda) + E(n) + M(d)

M(K^-) + M(p) - M(&Lambda) - B.E.(⁴He) = K(&Lambda) + K(n)

M(K^-) + M(p) - M(&Lambda) - B.E.(⁴He) + B.E.(d) = K(&Lambda) + K(n)

The updated N&Lambda invariant mass spectra and K(N)-K(&Lambda) correlation are shown below.

(Top) 2D correlation between proton(horizontal) and &Lambda(vertical) kinetic energy, being shown together with the kinematical limit, x+y = 288 MeV. (Bottom)p&Lambda invariant mass spectra, with(red:cos(p&Lambda).le.-0.95, green:cos(p&Lambda).gt.-0.95)/without(black) cos(p&Lambda) selection. Mass threshold ~2341.9 MeV/c² is represented by a red arrow.

(Top) 2D correlation between neutron(horizontal) and &Lambda(vertical) kinetic energy, being shown together with the kinematical limit, x+y = 288 MeV. (Bottom)n&Lambda invariant mass spectra, with(red:cos(n&Lambda).le.-0.95, green:cos(n&Lambda).gt.-0.95)/without(black) cos(n&Lambda) selection. Mass threshold ~2343.2 MeV/c² is represented by a red arrow.