Today's Progress 22. July. 2006

Proton ID function on PB/NT arm

Here, we exactly define the proton ID function on PA-PB-NT system.

Formalization

PAPB-measured inverse velocity, 1/beta(PA-PB) which is interpreted as the inverse velocity after penetrated the PA, has a direct relationship with total-energy-deposit on PB/NT. Due to the saturations of the light outputs of organic scintillators and (perhaps) PMT, measured total-energy-deposit, T.E(PB/NT), does not necessarily coincide with the depositted energy which can be easily calculated for stopped proton from its velocity. The situation is formulated as

T.E(PB/NT) = f(1/beta(PA-PB)) .

It should be noted that PB gain is tuned by stopped K^+ events, while NT gain is tuned by selecting Kmu2 events of stopped K^+, by the comparison between detected and simulated (for the simulated results, see, here) Landau peak positions.

Here, we determine the function f(x) from the data by a somewhat phenomenological way. The procedures are:

1. Pick up proton events graphically.

2. Fit the averaged correlation between T.E(PB/NT) and 1/beta(PA-PB), and define the function f(x) by the fitted function.

3. Define the PID function by

PID= T.E(PB/NT) - f(1/beta(PA-PB)) (MeVee).

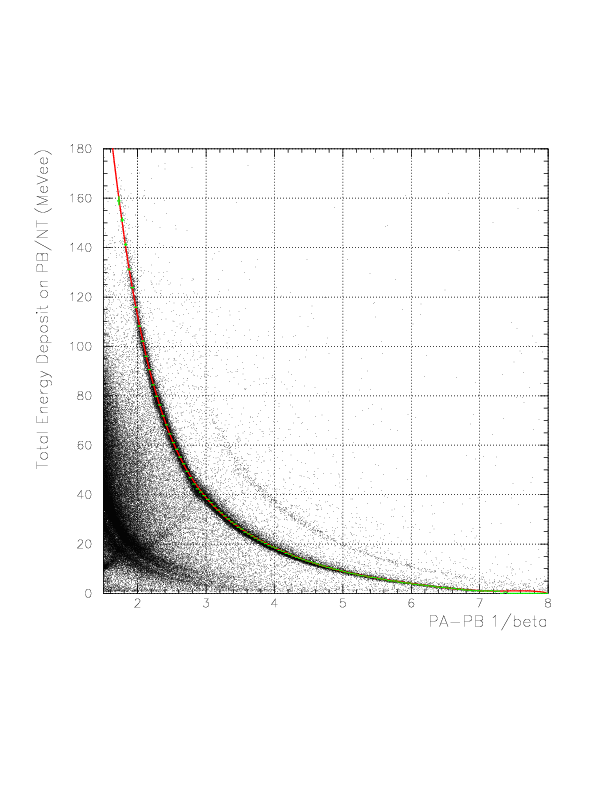
The global view of the correlation between inverse-velocity and total-energy-deposit for proton. The y-avaraged histgram (profile) for the proton component and its fit result are overlayed with green and red, respectively.

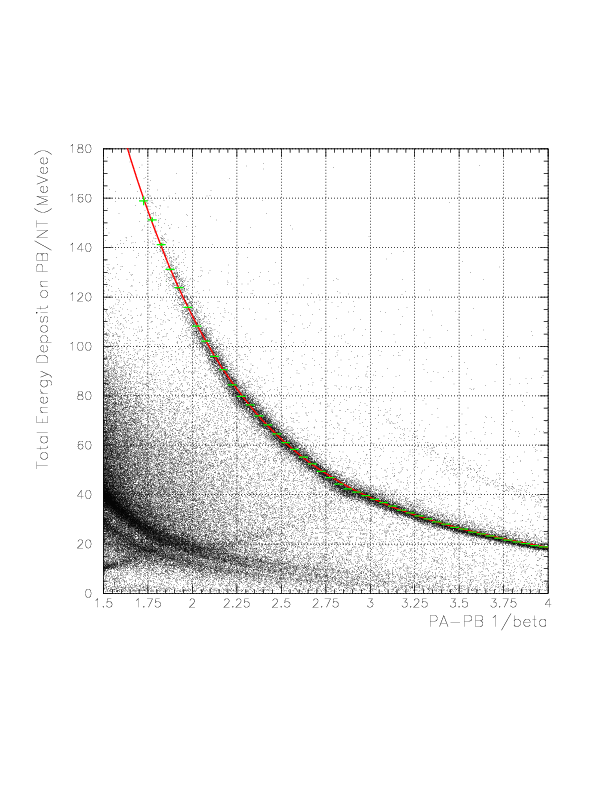
Smaller inverse velocity region of the correlation between inverse-velocity and total-energy-deposit for proton. Proton event exist from 1/beta=1.70 .

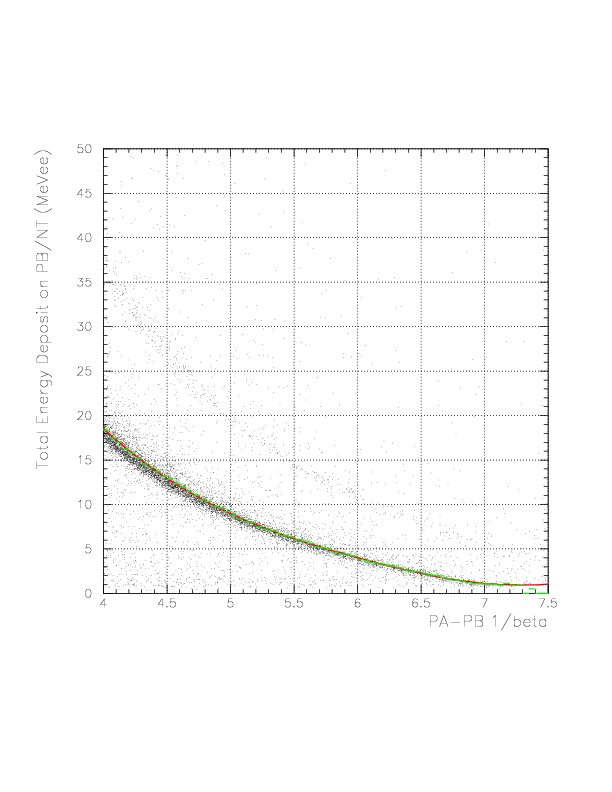
Larger inverse velocity region of the correlation between inverse-velocity and total-energy-deposit for proton. Proton events exist up to 1/beta=7.30 .

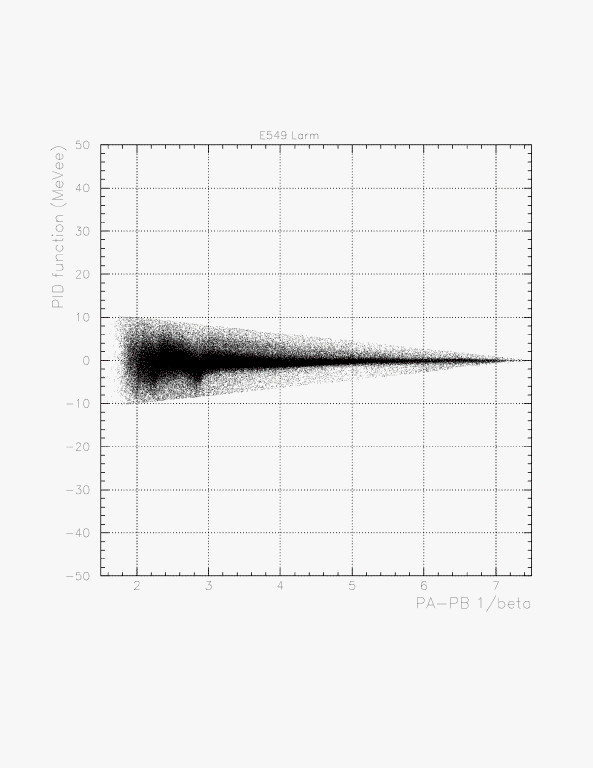
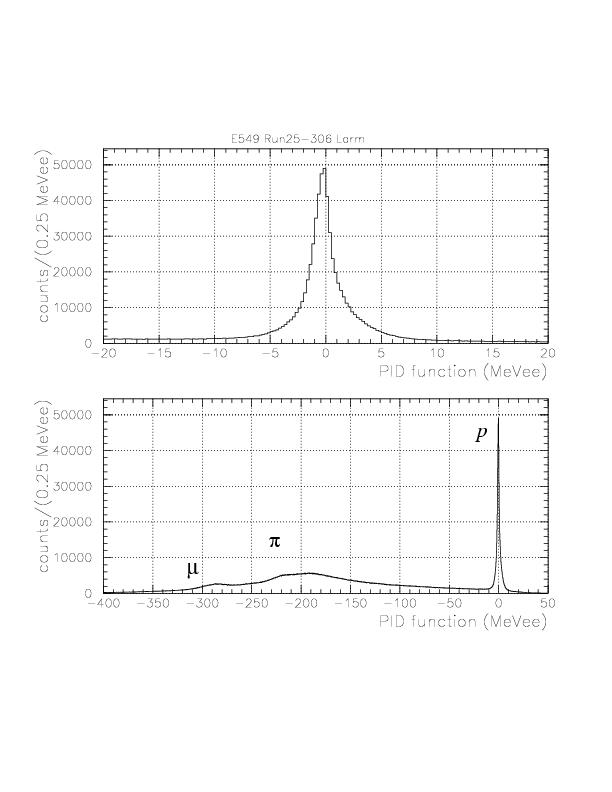
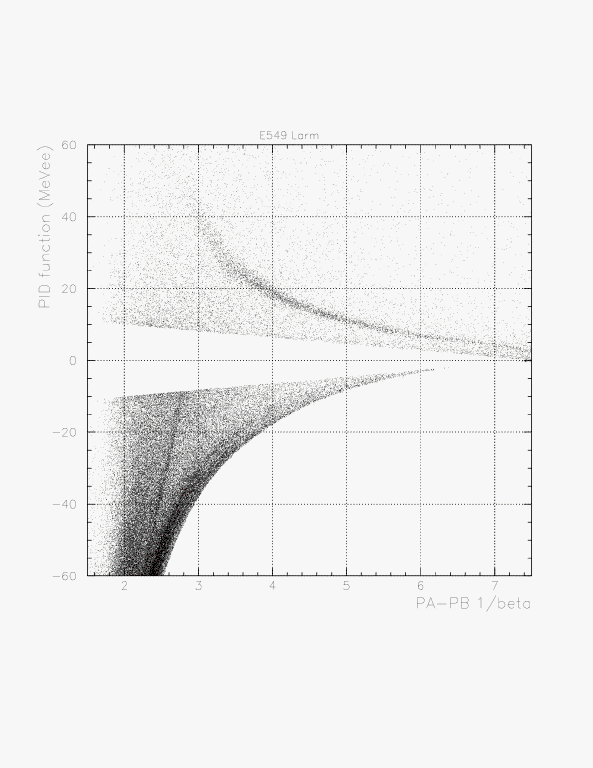
Local (top) and global (bottom) shape of the distribution of the PID function for Larm. On the bottom, mu/pi component is clearly seen.

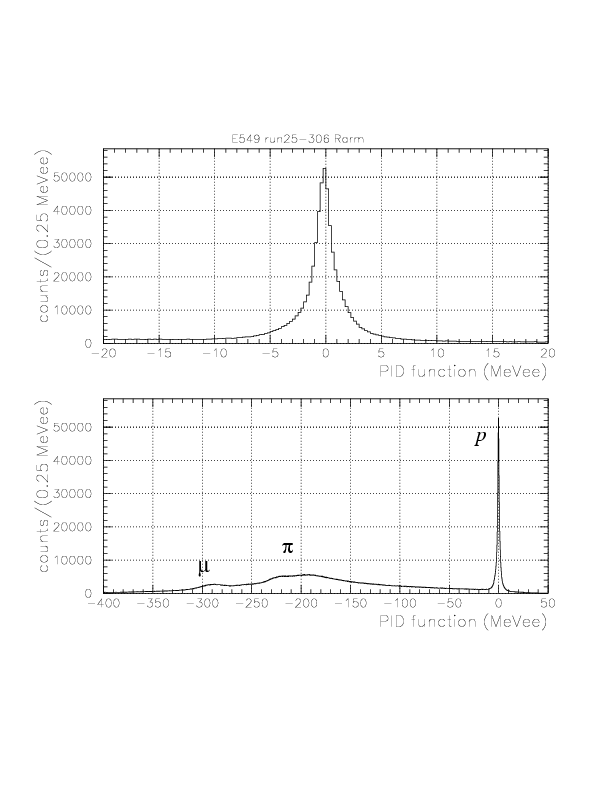
Local (top) and global (bottom) shape of the distribution of the PID function for Rarm.

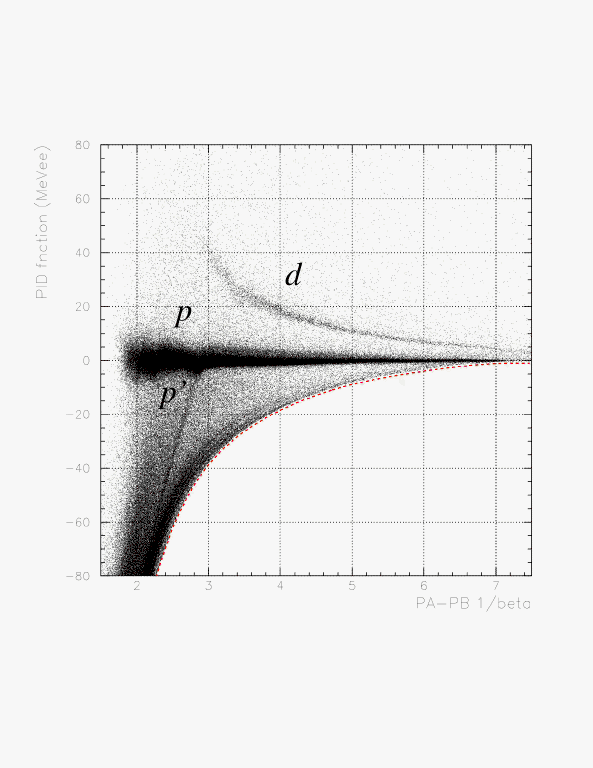
Definition of the 'permissible region'

It is expected that the width of the PID function is strongly 1/beta-dependent. Therefore, better proton selection is achieved not by a simple 1-dimensional gate on the function, but taking the dependence into accpunt.

The correlation between 1/beta (horizontal) and PID function (vertical) for Larm. -f(ibeta) is represented by a red dashed curve. The dependence of the width on the inverse beta is clearly seen.

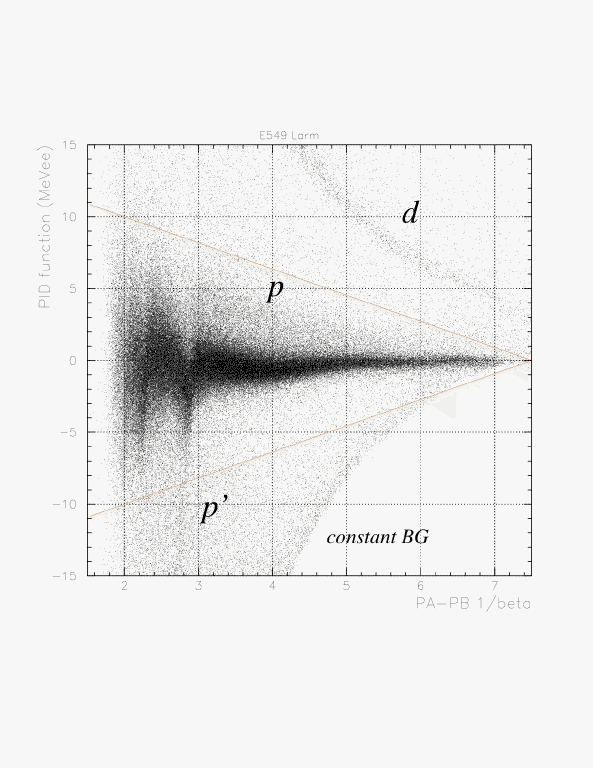
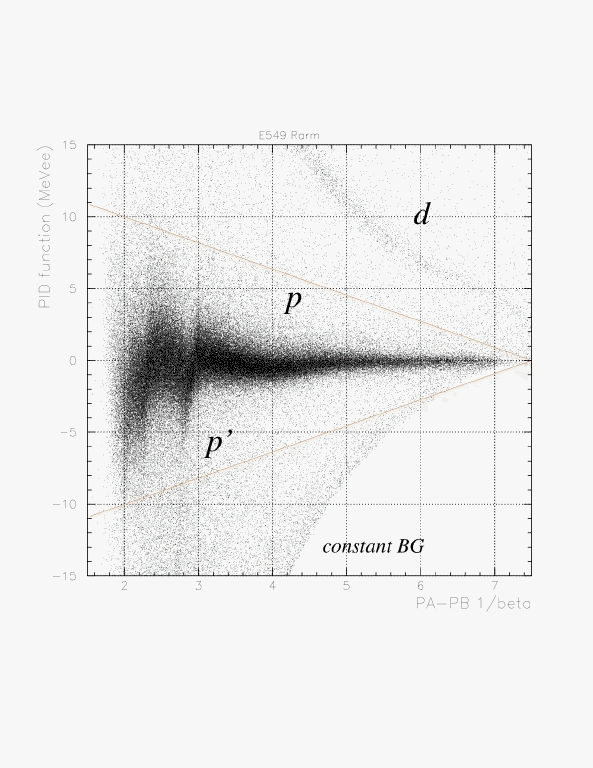
In order to select the 'proton' by 1/beta-dependent way, we introduce a phenomenological function, g(1/beta) as the straight line passing through two points (1/beta, PID) = (7.5, 0.),(2.0, 10.),

g(1/beta) -0.0= (0.0-10.0)/(7.5-2.0)*(1/beta-7.5).

Then, we define the 'proton' events by the condition,

|PID| < g(1/beta).

The event selection is show below arm-by-arm.