Today's Progress 20. June. 2006

Tune of T0 gain variation/nonlinearity - finalization

We solve the T0 non-linearity in by the following way:

1. Simulate the expected energy loss on T0 as the function of stopped vertex z position for Kaon. Also, peak position by pi beam is simulated.

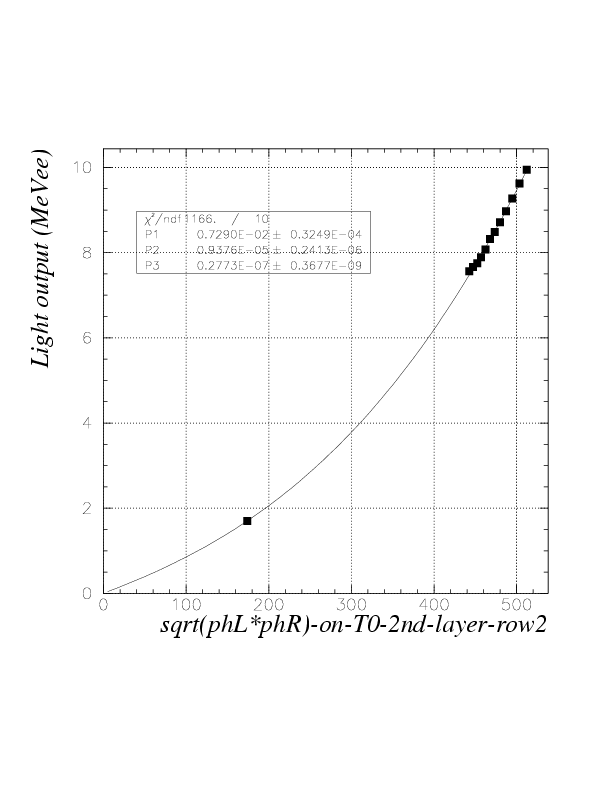
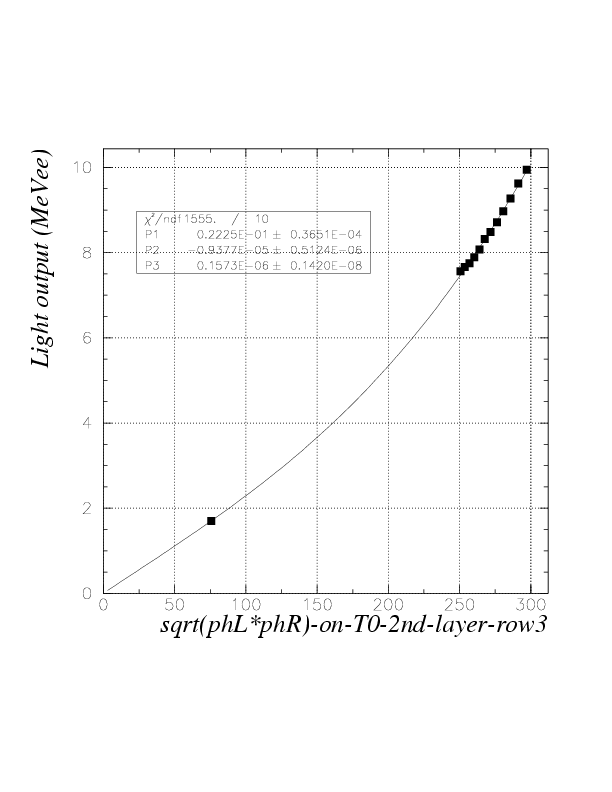
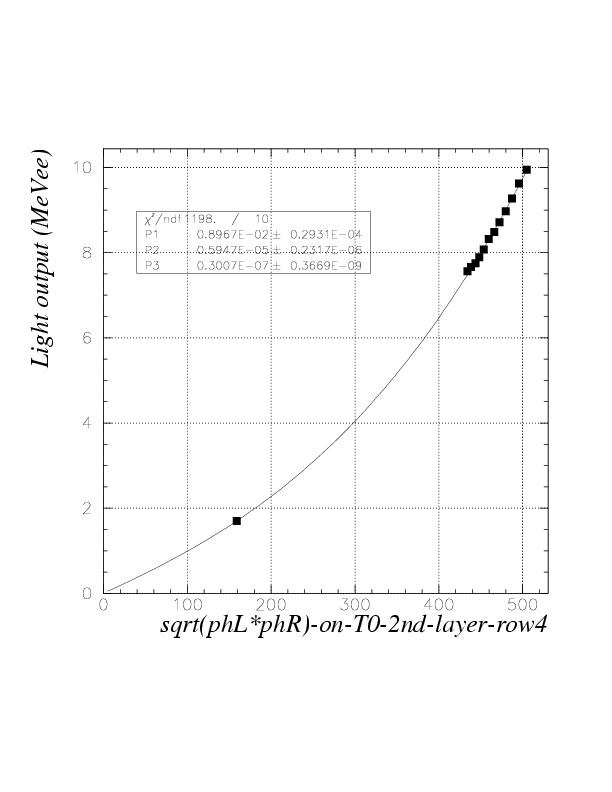
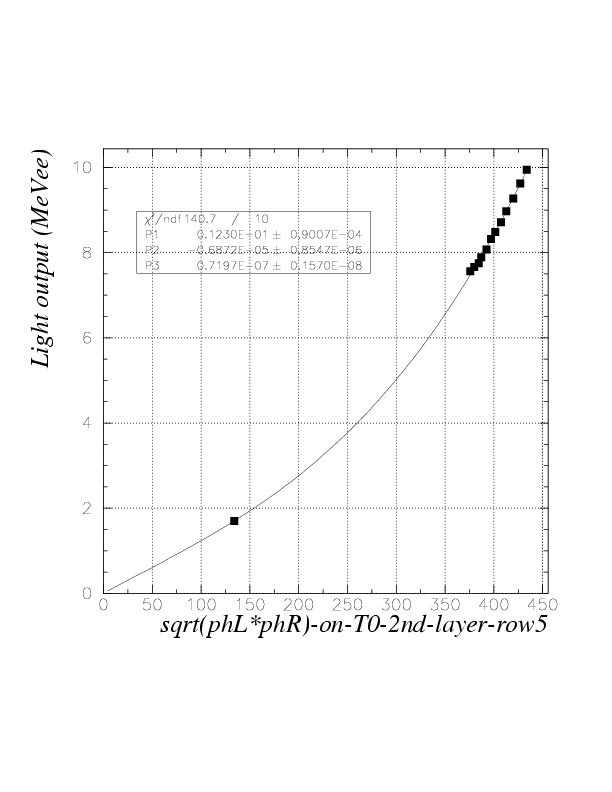
2. By plotting the simulated energies (MeVee) as the function of detected sqrt(phL*phR) for obtained data points and fitting by relevant functions, we obtain segment-by-segment sqrt(phL*phR) to energy (MeVee) convertion function, fi(E), as

fi=fi(sqrt(phL*phR))

. The index is for segment, first variable is run number (Note that we first determine fi at run 136). The function is determined with a constraint of "value 0 for sqrt(phL*phR)=0", to let it be globally appricable. Practically, 3rd order polinomial was necessary and enough to reproduce obtained data points. The fitting results are exhibitted below.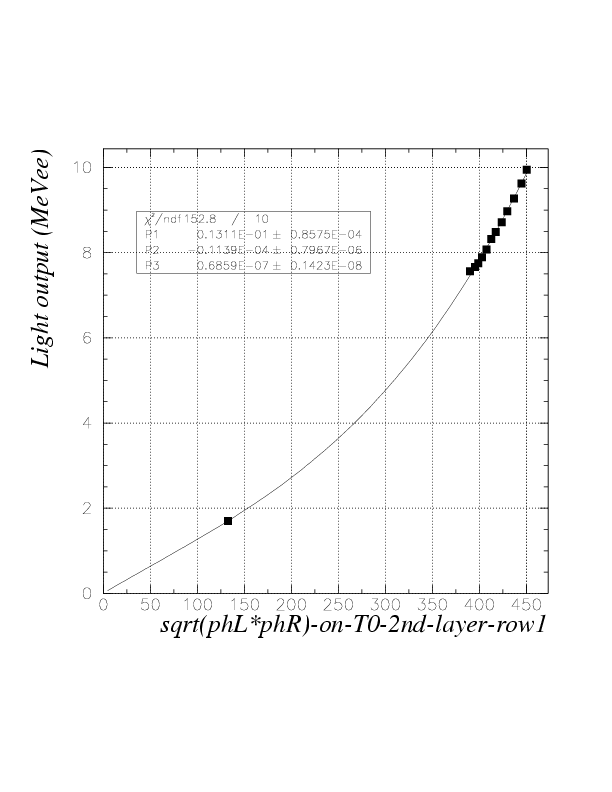

Now, correlation between energy on T0 2nd layer (MeVee) vs vertex z (cm) is as below.

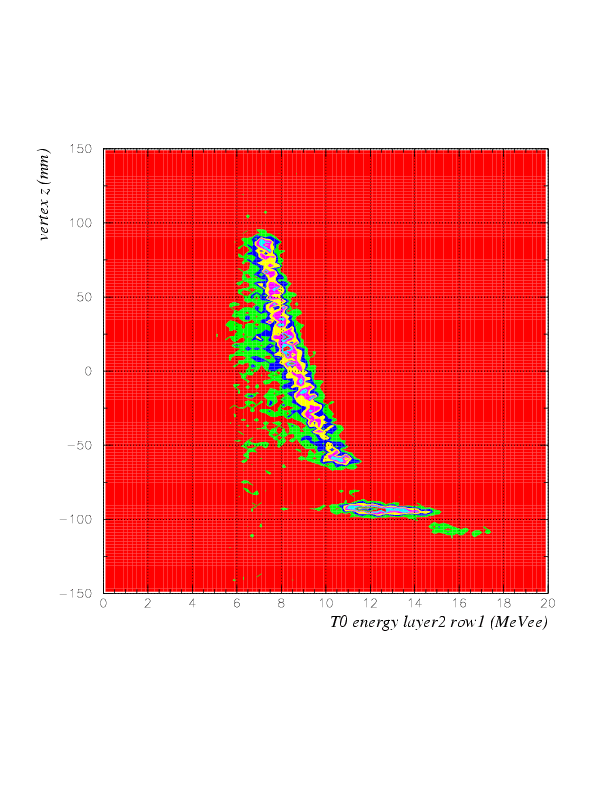
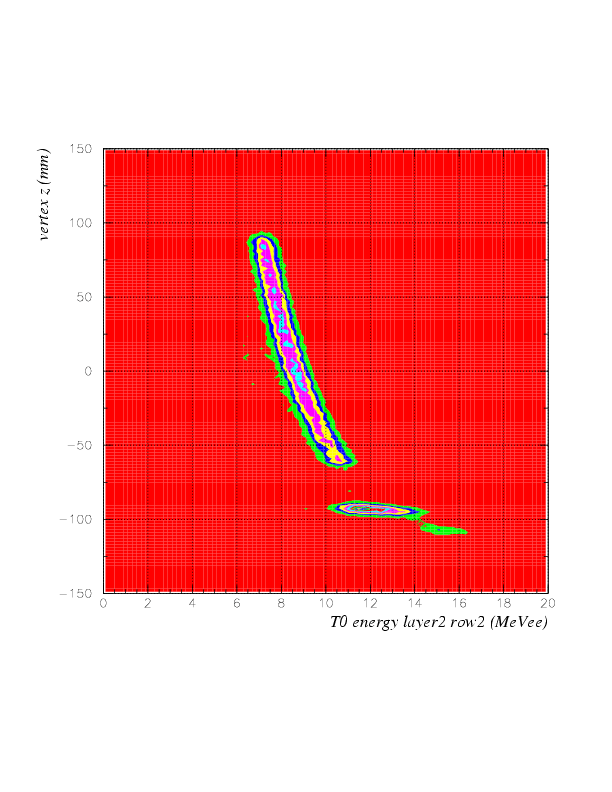
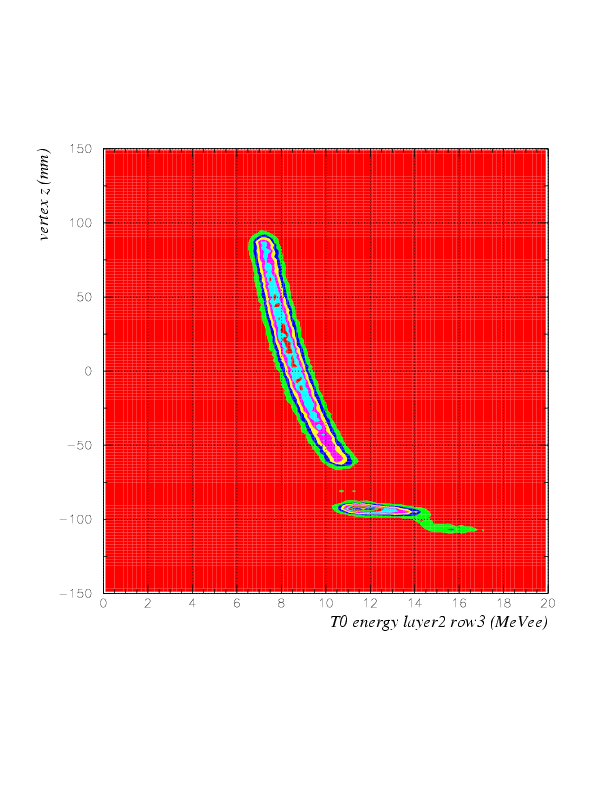
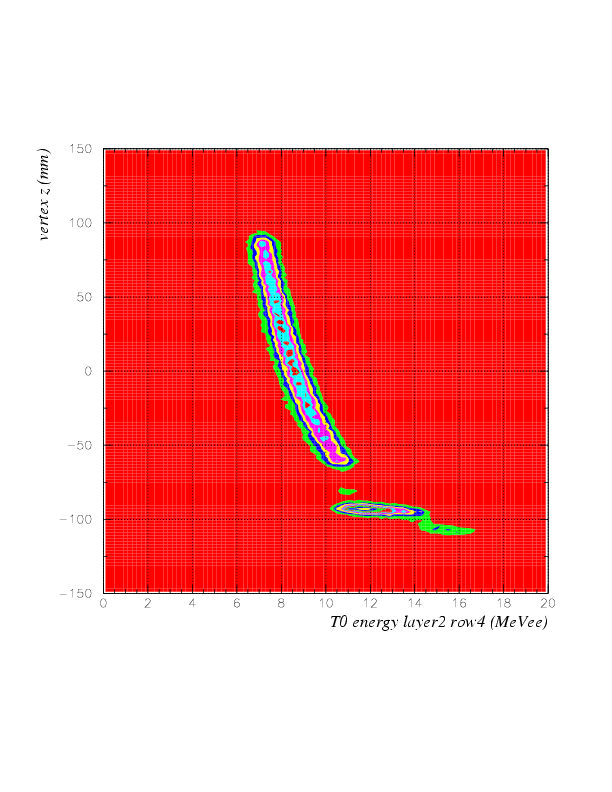
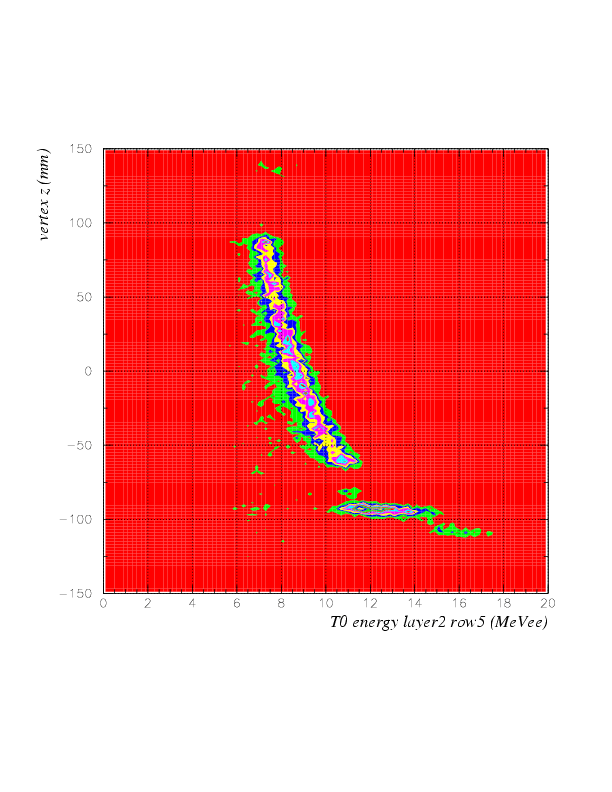
Segment-by-segment correlation between T0 energy (MeVee, horizontal) VS vertex z(cm, vertical) at run 136.

Since T0 nonlinearity is successfully solved, now we can introduce "ID function" of stopped K events. The ID function is constructed as a difference,

DeltaE - f(vz)

, between detected energy (DeltaE) and a 3rd order polinomial to fit the resultng energy-vertex correlation (f(vz)) shown below.

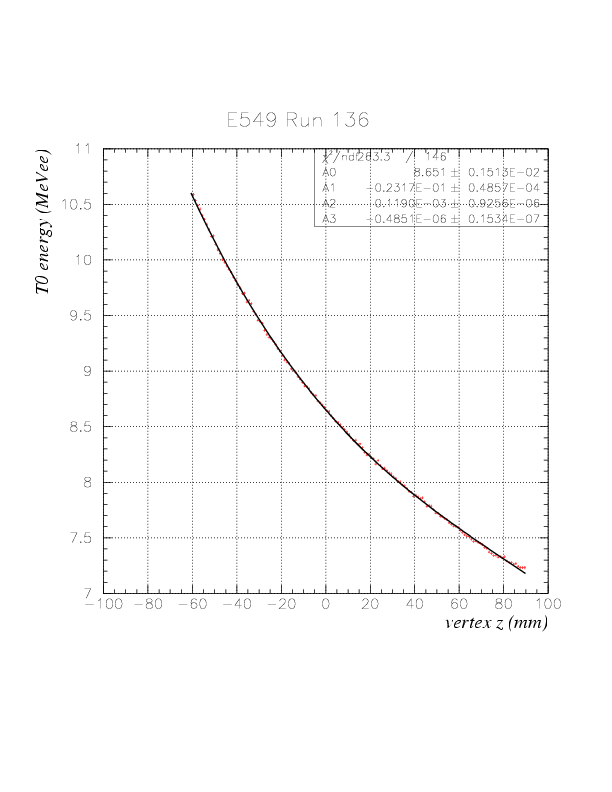
The resulting distribution of ID function and its correlation with vertex z for K^+ are as shown below .

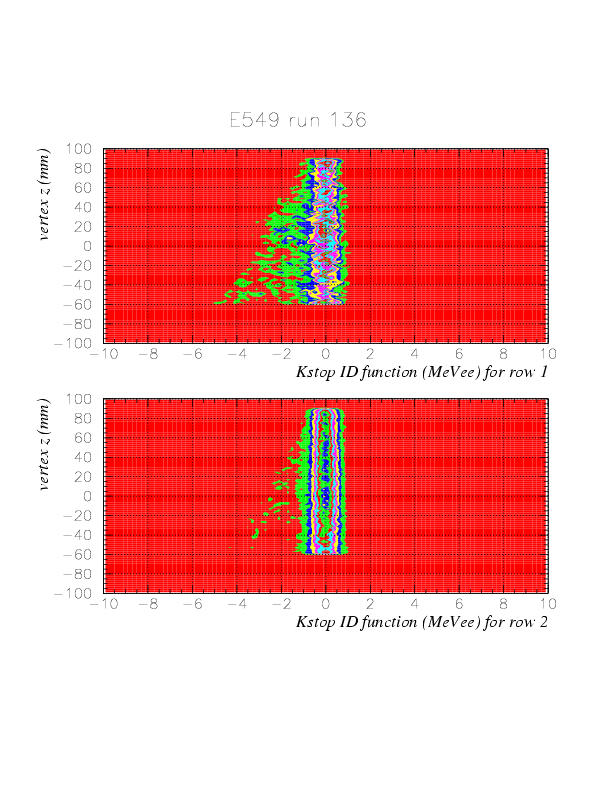
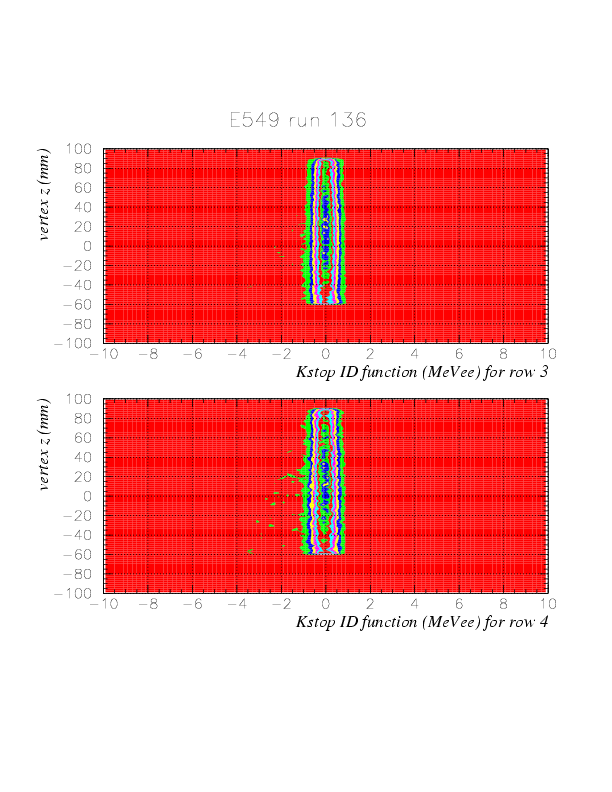
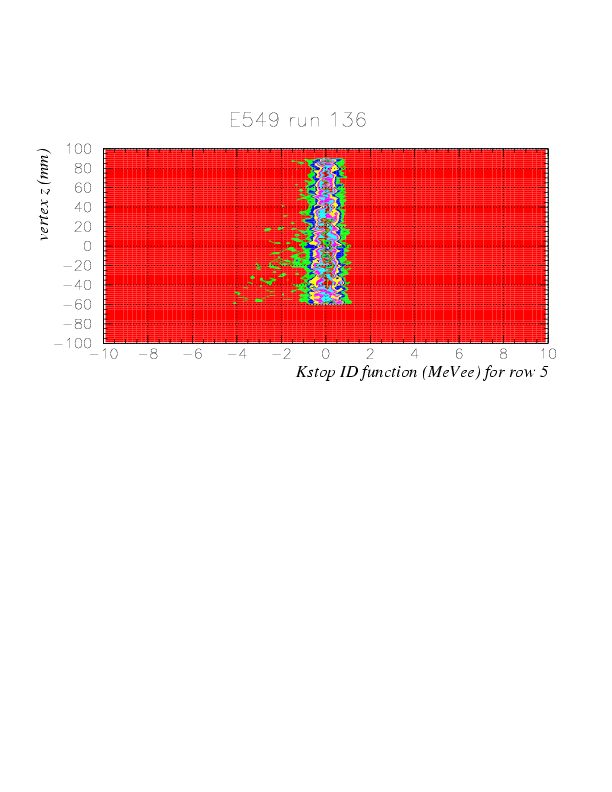
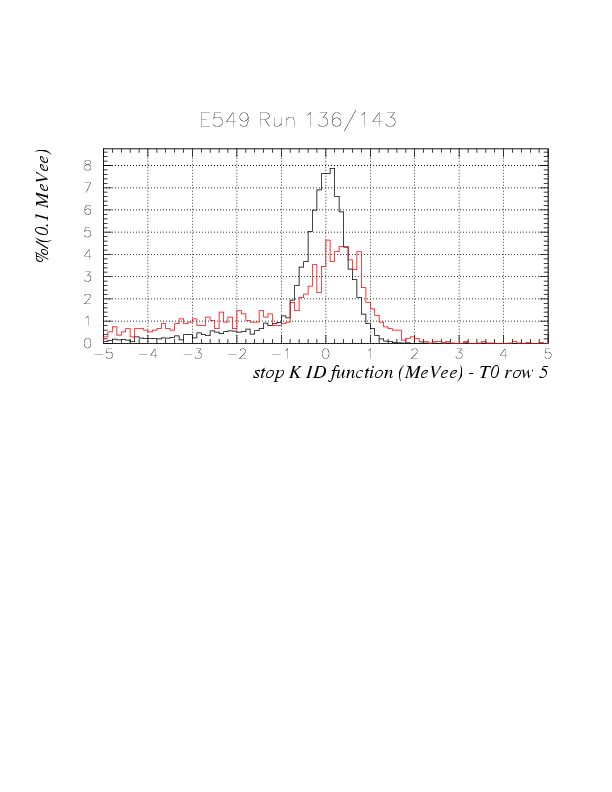
The comparison between ID function for run 136 (K^+) and 143 (K^-) are shown below. IDfunc > -1. may work well. The shift of the central position can be attribued to the gain drift discussed nextly.

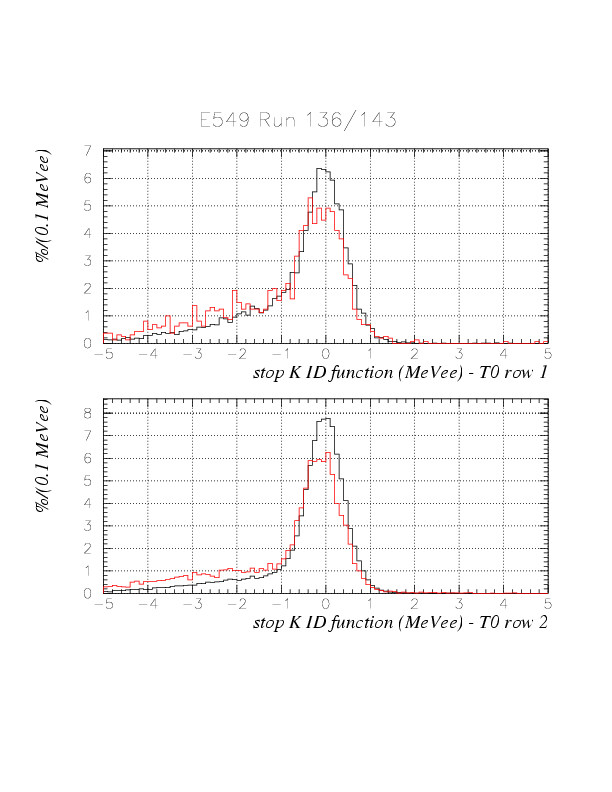
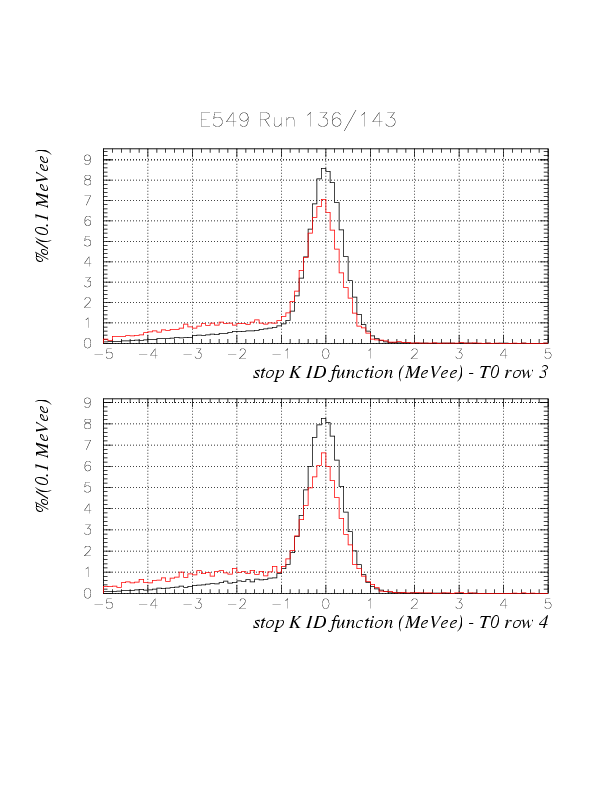
3. Run-by-run gain variation is then considered. Now, the gain variation is studied as of the variation of the peak position of the sqrt(phL*phR) when kaon stopped at -5~+5 . Let we define the peak position for vz:-5~5 as E_0(Nrun). Then, the convertion function for run Nrun is defined as

fi(Nrun,E) = fi(136,E')

, where E' is defined as

E' = E*(E_0(136)/E_(Nrun)).

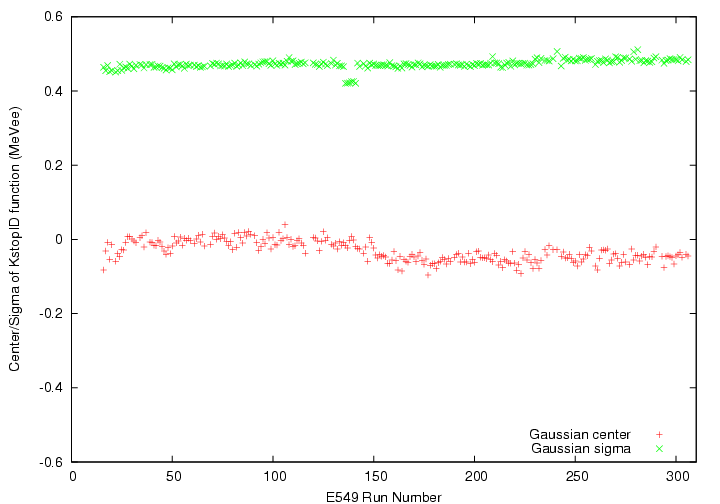
By this correction, the run-by-run variation of KstopID function can be fully stabilized, as shown below.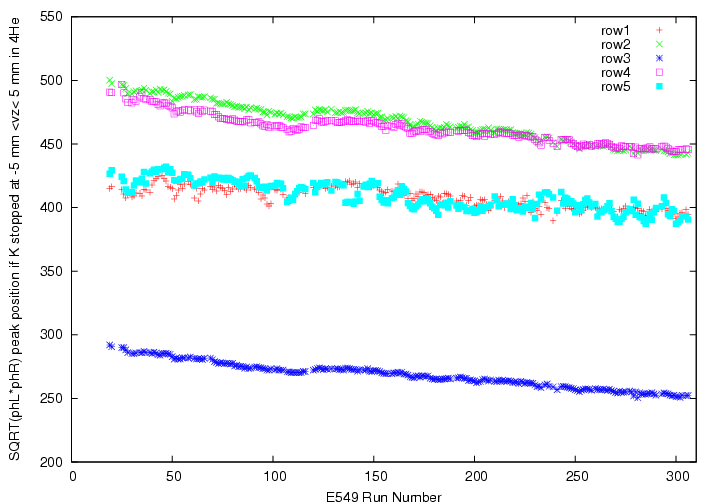
Run-by-run segment-by-segment gain variation for T0 2nd layer. In order to avoid to be affected by possible change of beam condition, now stop K events at -5. < vz < 5. are slelected. Note that jump for K^+ runs has been disappeared - that jump is attributed to the different beam position/angle/momentum distributiuons of K^+ beam.
Gain walk of T0 2nd layer
Run-by-run variation of the KstopID function, represented by fitted Gaussina center and sigma.
Stability of the Kstop ID function
A comparison of distributions of ID function between run 141 (K^+, red)/143(K^-, black).
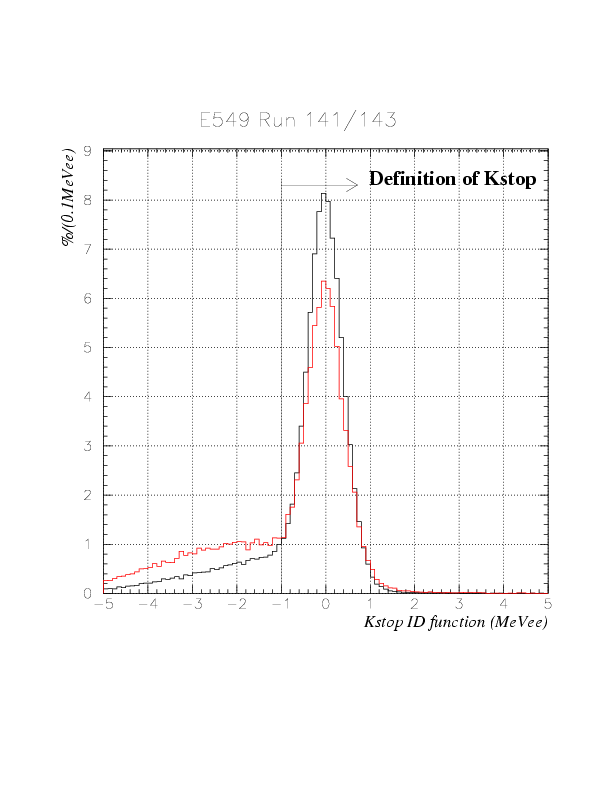
Comparison of the Kstop ID function

Hereafter, 'Kstop' event is selected by

KstopID > -1. (MeVee),

at least if T0-PA TOF is not available.