Why do we need spline correction for VDC tracking?
Residual distributions for various slope values for cosmic ray.... for VDCtop y-x tracking.
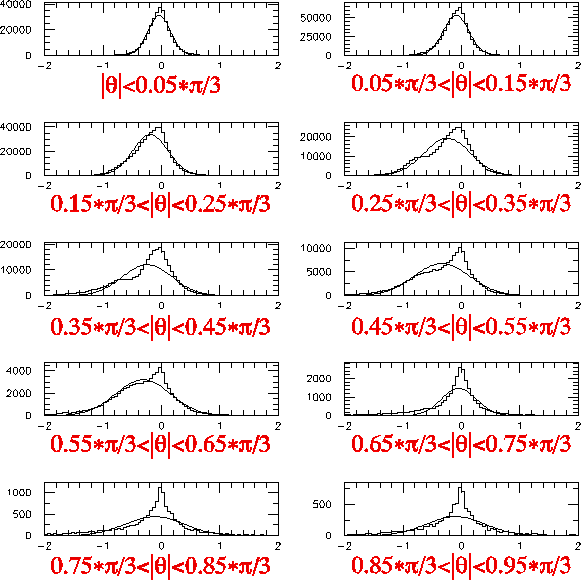
The strong dependence of the resolution (and systematic deviation) on the slope is now clearly seen. The dependence of the resolution (defined by Gaussian sigma obtained by functional fitting) on the slope is shown below, for cosmic ray measured in run 117 to 128.
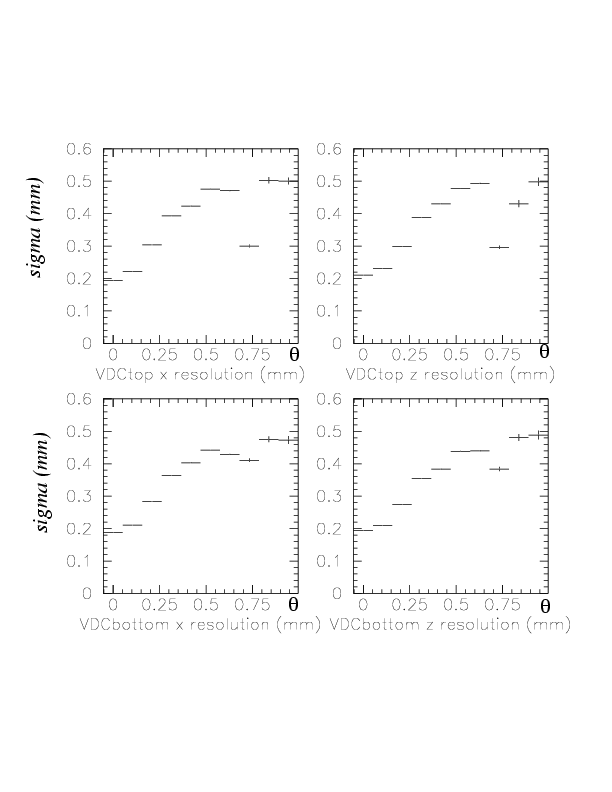
This sad situation can be improved if we introduce slope-dependent correction term for drift length.
For the detail of the realistic procedures, refer to the corresponding part of this thesis .As the source, cosmic ray maeasurement of run 117 to 128 are adopted, and used.
The resulting residual distributions for various slope values for cosmic ray (run 117 to 128) for VDCtop y-x tracking are shown below for 3rd stage iterative tracking.
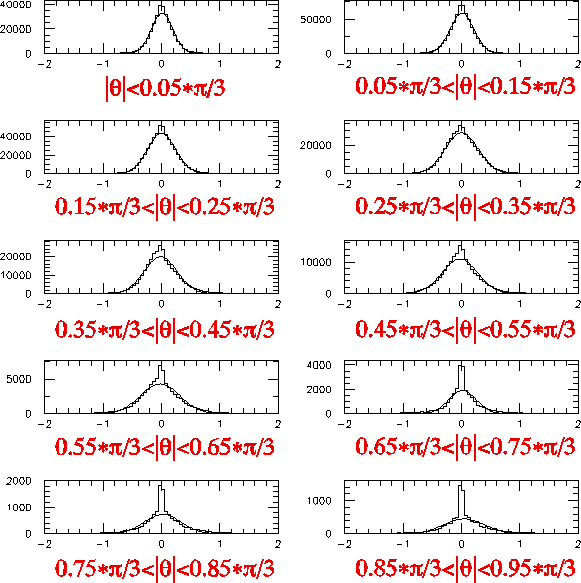
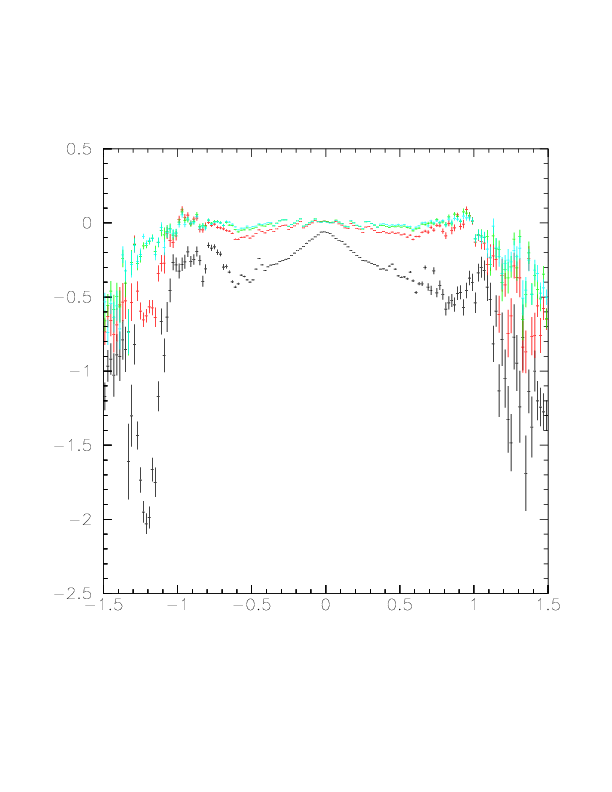
Accordingly, strong theta-dependence of the resolution is gradually improved with the stage of the spline correction, as exhibitted below. Black:no correction, red:1st stage, green;2nd stage, sky-blue;3rd stage. BUT it cannot be complately removed. Practically, we will use stage 2.
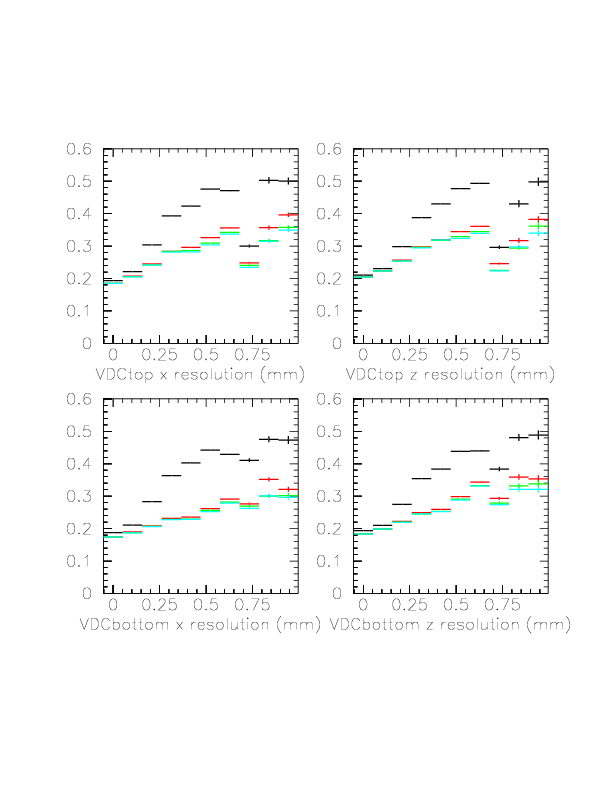
The correlation between slope (arctan(a), abscissa) and mean of fit residual (ordinate), and its improvement with the stage of spline-correction is clearly seen in the cosmic-ray tracking result (run117~128). Black:no correction, red:1st stage, green;2nd stage, sky-blue;3rd stage.
Subjects to be done on tracking (in order) ....
1. VDC tracking: Completed besides the long-term stability of the spline correction - see, 0812 .
2. PDC tracking: Under construction. Shift correction, time-to-time dt-dx reconstruction are not done yet -
3. VDCbottom relative rotation and position shift determinations by cosmic ray.
4. BLC relative rotation and position shift by K^+-VTC triggered run.